BACKGROUND
When constructing regression models, there are two approaches to handling confounders: (1) conditional and (2) marginal approaches.(1) The conditional approach handles confounders using stratification or modeling (e.g., adding covariates to be regressed to the outcome). Whereas, the marginal approach uses weights to balance the confounders across treatment exposure levels.(1–5) In conventional regression models, the exposure is regressed to the outcome controlling for potential confounders. However, in longitudinal data, time-varying confounders can result in biased estimates of the model parameters if not properly adjusted. This gets more complicated when we have a time-varying exposure in the model to account for.
In panel data analysis or longitudinal data analysis, adjusting for time-varying exposure and time-varying confounders are critical to reducing bias. Additionally, there are time-dependent relationships between the confounders and exposure that need to be considered when adjusting for longitudinal regression models. In this article, we will focus on the marginal approach in terms of using the inverse probability of treatment weights fitted to a marginal structural model.
This article was published on RPubs with the corresponding R code using RMarkdown and can be located at this link.
TIME-DEPENDENT RELATIONSHIPS
In Figure 1, the time-dependent relationships between times 1 and 0 for the treatment variable are indicated by the arrows (We look at the relationships across two time points. In actual longitudinal data, there may be more than two time points to consider). Notice how the Outcome at time==0 is a confounder for the relationship between Exposure and Outcome at time==1.
Figure 1. Time-dependent relationships between the exposure and outcome variables.
Conventional methods to perform longitudinal data analysis such as linear mixed effects models and generalized estimating equations models are capable of handling time-varying covariates. However, in the case of a time-varying elements, the probability of treatment exposure is invariably different across time, which requires application of time-varying weights on the unit of analysis (e.g., individual subjects).
We can address this issue by applying inverse probability of treatment weights (IPTW) to the observations, which are then fitted to a marginal structural model (MSM).(4,5) IPTW are used to make the exposure at time 0 and 1 independent of the confounders that occur beforehand and allow us to generate a causal interpretation between the treatment exposure on the outcome.
DESCRIPTION OF METHODS
IPTW are weights assigned to each observation across time conditioned on the previous exposure history, which are then multiplied to generate a single weight for a subject. Similar to conventional propensity score estimation, IPTW is generated using either a logit or probit model that regresses covariates to a treatment group (exposure) variable. With IPTW, the previous exposure history is incorporated to the propensity score estimation, which is time-varying.
Standardized weights in a longitudinal setting are estimated as
where A is the exposure for subject i at time t_ij (time points range starting at k = 0 to k=j). The numerator contains the probability of the observed exposure at each time point (a_ik) conditioned on the observed exposure history of the previous time point (a_ik-1) and the observed non-time varying covariates (v_i). The denominator contains the probability of the observed exposure at each time point conditioned on the observed exposure history of the previous time point (a_ik-1), the observed time-varying covariates history at the current time point (c_ik), and the non-time varying covariates (v_i).
In standardized weights, the time-varying confounders are captured in the denominator but not in the numerator. However, the non-time varying (also known as fixed-time) covariates are captured in both the numerator and denominator to stabilize the weights. Using stabilized weights is preferable to non-standardized weights, which are not discussed in this article.
Some statistical software are unable to handle time-varying weights; hence, a single weight for each individual needs to be estimated. Once the standardized weights for subject i at time t_ij are calculated, a single weight is estimated by multiplying all the standardized weights across the time points, which is then applied in a marginal structural model for subject i.
There are several key assumptions that must be made in order for IPTW methods to generate causal interpretation between the exposure and outcome (Thoemmes and colleagues provides a detailed explanation in their paper)(5):
1) No unmeasured confounding
2) Positivity
3) Correct specification of the IPTW
Given these assumptions are met, using IPTW fitted to an MSM can yield causal inference between the treatment exposure and outcome. This method is flexible enough where it can be applied to a linear mixed effects model, generalized estimating equation model, and survival model. Gerhard and colleagues used this approach (marginal structural Cox model) to estimate the treatment effects of antihypertensive therapy in a non-randomized trial.(6) Hernan and colleagues used a marginal structural Cox proportional hazard model to estimate the treatment effect of zidovudine and Pnuemocystis carinii therapy on survival of HIV-positive homosexual males in a non-randomized trial.(4)
MOTIVATING EXAMPLE
This article will use CRAN R program statistical software to perform the IPTW fitted to an MSM. We will use the data that was simulated using the following R commands.
#set seed to replicate results set.seed(12345) #define sample size n <- 2000 #define confounder c1 (gender, male==1) male <- rbinom(n,1,0.55) #define confounder c2 (age) age <- exp(rnorm(n, 3, 0.5)) #define treatment at time 1 t_1 <- rbinom(n,1,0.20) #define treatment at time 2 t_2 <- rbinom(n,1,0.20) #define treatment at time 3 t_3 <- rbinom(n,1,0.20) #define depression at time 1 (prevalence = number per 100000 population) d_1 <- exp(rnorm(n, 0.001, 0.5)) #define depression at time 2 (prevalence = number per 100000 population) d_2 <- exp(rnorm(n, 0.002, 0.5)) #define depression at time 3 (prevalence = number per 100000 population) d_3 <- exp(rnorm(n, 0.004, 0.5)) #define tme-varying confounder v1 as a function of t1 and d1 v_1 <- (0.4*t_1 + 0.80*d_1 + rnorm(n, 0, sqrt(0.99))) + 5 #define tme-varying confounder v2 as a function of t1 and d1 v_2 <- (0.4*t_2 + 0.80*d_2 + rnorm(n, 0, sqrt(0.55))) + 5 #define tme-varying confounder v3 as a function of t1 and d1 v_3 <- (0.4*t_3 + 0.80*d_3 + rnorm(n, 0, sqrt(0.33))) + 5 #put all in a dataframe and write data to harddrive to use later in e.g. SPSS df1 <- data.frame(male, age, v_1, v_2, v_3, t_1, t_2, t_3, d_1, d_2, d_3) write.table(round(df1,11),"data1.csv", row.names = FALSE, quote = FALSE)
A little data manipulation was done to make treatment in the following period equal to 1 if the previous period was also equal to 1. In other words, E[Treatment=1, time=1 | Treatment=1, time=time-1]. Age was rounded to the nearest whole number. You can download the *CSV file here.
The dataset contains variables for id, male, age, treatment (t), outcome (d), time-varying covariate (v), and time. Exploring the dataset set, we see the structure as:
There are 2000 individuals with three repeated measures of the t, v, and d variables. The t variable represents the Treatment exposure, which is time-varying. The v variable represents an arbitrary time-varying covariate. And the d variable is the outcome (dependent) variable, which is also time-varying. Non-time varying covariates include the age at baseline and the gender of each individual.
LONGITUDINAL DATA ANALYSIS APPROACH
Generalized estimating equations (GEE) were constructed to evaluate the impact of the treatment (t) on the outcome (d) and to handle the time-varying covariate (v) in the panel dataset. Since the outcome was a continuous variable, a generalized linear Gaussian family with identity link was used. Auto-regressive (AR1) correlation structure was selected since this was a time series (panel) data; we expected the correlation to decay as the outcome values were farther away from the time of interest.
We will need the following packages:
geepack
survey
ipw
reshape
deplyr
The following R code was used to generate the IPTW and fitted to a MSM using GEE.
####################################################################### # Install the required packages ####################################################################### library(geepack) library(survey) library(ipw) #library(foreign) #library(multcomp) #library(gee) library(reshape) library(dplyr) ####################################################################### #Estimate ipw weights (time-varying) ####################################################################### # estimate inverse probability weights (time-varying) using a logistic regression w <- ipwtm( exposure = t, family = "binomial", link = "logit", numerator = ~ factor(male) + age, denominator = ~ v + factor(male) + age, id = id, timevar=time, type="first", data = data_long_sort) summary(w$ipw.weights) iptw = w$ipw.weights # Add the iptw variable onto a new dataframe = data2. data2 <- cbind(data_long_sort, iptw) ####################################################################### # Plot the stabilized inverse probability weights ####################################################################### ipwplot(weights = data2$iptw, timevar = data2$time, binwidth = 0.5, main = "Stabilized weights", xaxt = "n", yaxt = "n") ####################################################################### # confint.geeglm function (to generate 95% CI for the geeglm()) ####################################################################### confint.geeglm <- function(object, parm, level = 0.95, ...) { cc <- coef(summary(object)) mult <- qnorm((1+level)/2) citab <- with(as.data.frame(cc), cbind(lwr=Estimate-mult*Std.err, upr=Estimate+mult*Std.err)) rownames(citab) <- rownames(cc) citab[parm,] } ####################################################################### # GEE model #1.1 - GEE with cluster robust SE (no IPTW) ####################################################################### gee.bias <- geeglm(d~t + time + factor(male) + age + cluster(id), id=id, data=data2, family=gaussian("identity"), corstr="ar1") summary(gee.bias) confint.geeglm(gee.bias, level=0.95) ####################################################################### # GEE model #2 - IPTW fitted to MSM with clustered robust SE ####################################################################### gee.iptw <- geeglm(d~t + time + factor(male) + age + cluster(id), id=id, data=data2, family=gaussian("identity"), corstr="ar1", weights=iptw) summary(gee.iptw) confint.geeglm(gee.iptw, level=0.95)
We compared the findings from the convention GEE model without IPTW to the GEE model incorporating IPTW (Table). The differences are significant. In the standard GEE model, the treatment (t) is associated with a reduction in the outcome (d) by 0.012 units with a 95% confidence interval (CI) of -0.020 and 0.045, which is not statistically significant. Conversely, in the GEE model incorporating IPTW, the treatment (t) is associated with a reduction in the outcome (d) by 0.071 units with a 95% CI of -0.104 and -0.038, which is statistically significant.
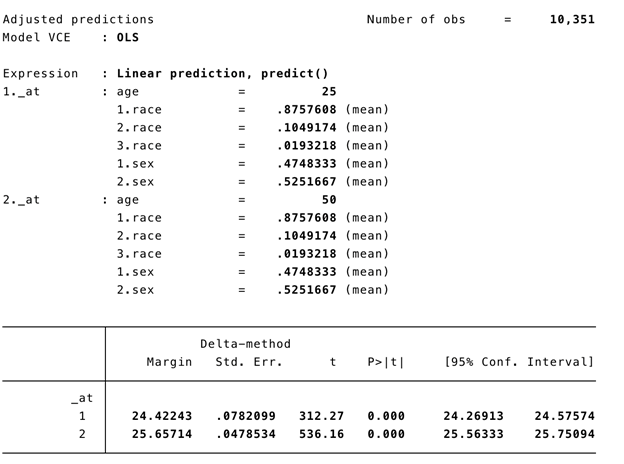
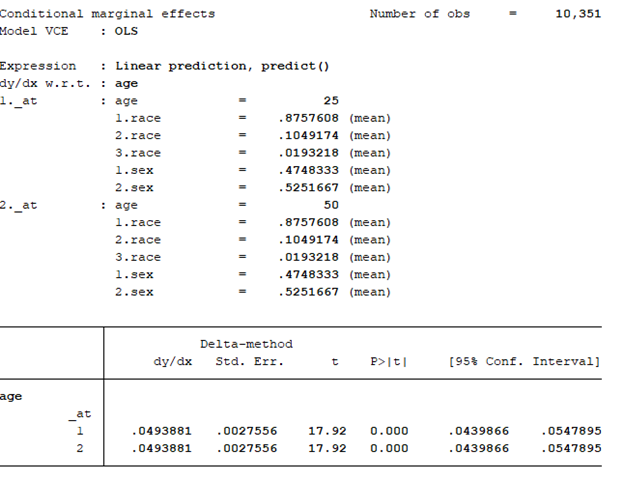
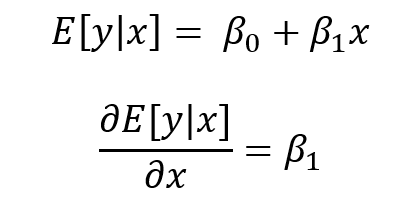CONCLUSIONS
Based on our findings, the IPTW fitted to a MSM (GEE model) resulted in a statistically significant reduction in the treatment on the outcome that would not have otherwise been captured in the conventional GEE model. Given that there are time-varying covariates (especially with the treatment variable), IPTW fitted to a MSM may yield important differences that would otherwise be unidentified with conventional methods. However, it is critical that all assumptions regarding the IPTW method are satisfied prior to accepting the model’s results.
REFERENCES
1. Williamson T, Ravani P. Marginal structural models in clinical research: when and how to use them? Nephrol Dial Transplant. 2017 Apr 1;32(suppl_2):ii84–90.
2. Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiol Camb Mass. 2000 Sep;11(5):550–60.
3. Hernán MA, Hernández-Díaz S, Robins JM. A structural approach to selection bias. Epidemiol Camb Mass. 2004 Sep;15(5):615–25.
4. Hernán MA, Brumback B, Robins JM. Marginal Structural Models to Estimate the Joint Causal Effect of Nonrandomized Treatments. J Am Stat Assoc. 2001 Jun 1;96(454):440–8.
5. Thoemmes F, Ong AD. A Primer on Inverse Probability of Treatment Weighting and Marginal Structural Models. Emerg Adulthood. 2016 Feb 1;4(1):40–59.
6. Gerhard T, Delaney JA, Cooper-DeHoff RM, Shuster J, Brumback BA, Johnson JA, et al. Comparing marginal structural models to standard methods for estimating treatment effects of antihypertensive combination therapy. BMC Med Res Methodol. 2012 Aug 6;12:119.
