Communicating data effectively with data visualizations - Part 5 (Colors)

Background

As we decide the type of chart we want to visualize our data with, we should also think about our color scheme. Color should represent the data value. We should be able to see a chart, identify the color that interests us and associate a value with it. However, it is easy to misidentify the data that the color is supposed to represent and it is also easy to confuse the magnitude of the difference between groups.

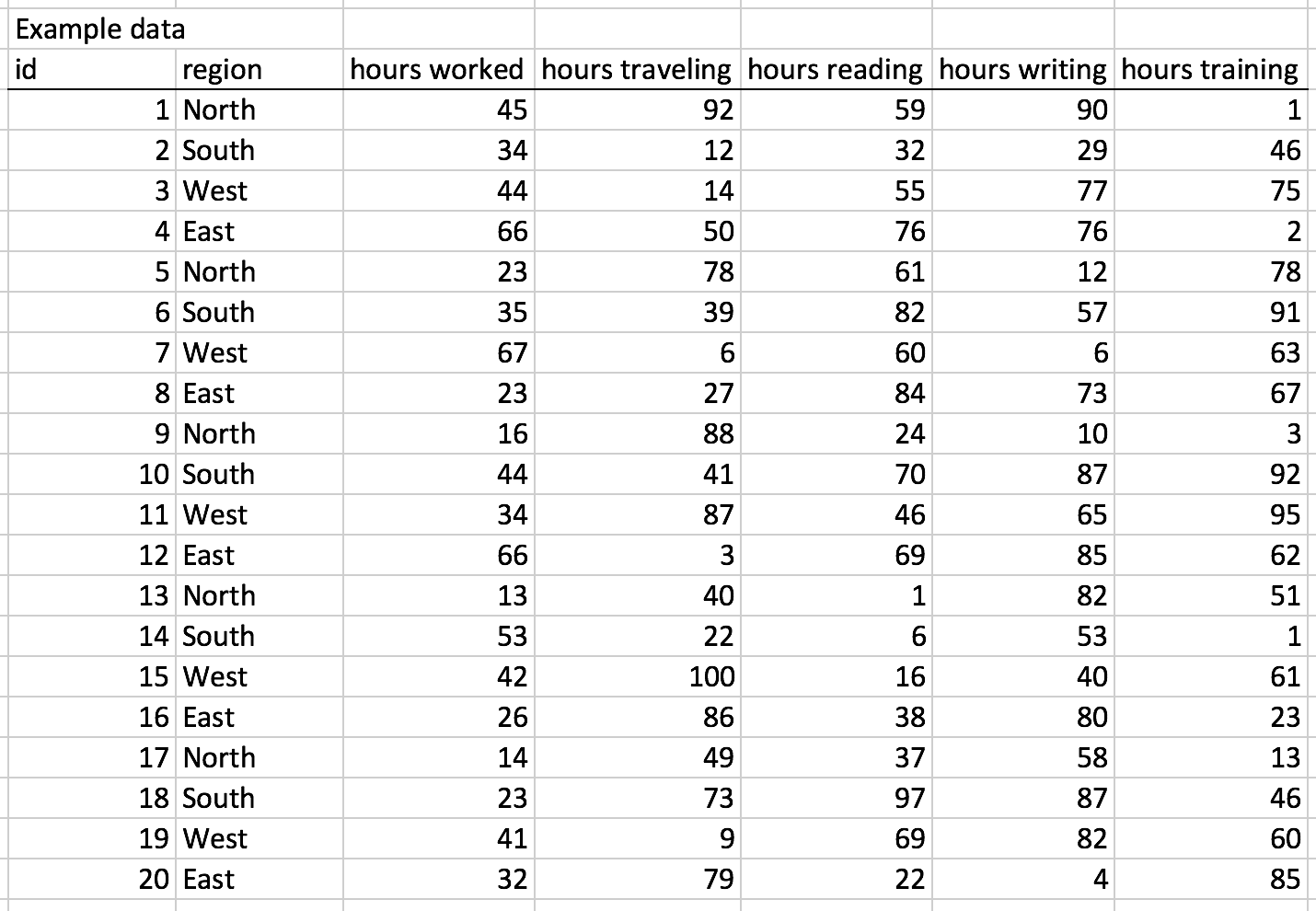
In this tutorial, we will discuss some basic elements of color theory that will help you to select the best color palette for your graphical presentations. We will use the following simple data and color schemes to illustrate some of these lessons (Figure 1). The X column denotes some arbitrary category that uses the alphabet and the Y column denotes the values associated with each category.

Figure 1. Example data used to illustrate the different color schemes.

Figure 2. Color schemes used in this example (single-hue color and rainbow color schemes).

 

Bias-Precision Tradeoff

There is always a tradeoff between bias and precision. Bias is associated with the ability to accurately identify the data value associated with the color. Precision is associated with the ability to correctly identify the data with little variation. Figure 3 illustrates the differences between the two.

Figure 3. Bias and Precision tradeoff.

For example, if you had a single-hue progression color scheme (blue), it is easy to identify the color that contains the higher value versus the color that contains the lower value. In Figure 4A, the darker shade of blue is associated with a higher value compared to the lighter shade of blue. However, it may not be easy when you have a rainbow color scheme because the values can be arbitrarily associated with a different color (Figure 4B). In other words, Figure 4A helps to reduce the bias while Figure 4B can generate a lot of bias.

Figure 4. Comparison between single hue color scheme and rainbow color scheme.

View fullsize

Additionally, Figure 4B is easier to distinguish between the groups. You can easily identify Group F compared to Group E because the colors are distinctly differentiable. However, in Figure 4A, it is very difficult to distinguish between Group F and Group E because the shades of blue associated with both groups appear similar. Therefore, the ability to precisely detect the differences in the groups is limited by the single-hue color scheme (Figure 4A) compared to the rainbow color scheme (Figure 4B).

Another way to look at these principles is to think about the concurrence between the true value and the estimated value. Suppose you were given these color schemes and asked to estimate the correct value. How do you think you’ll do? Would it be easier to estimate the true value from the single-hue color scheme or the rainbow color scheme?

Figure 5. Performance of color schemes according to estimated and true values.

View fullsize

I generated data in Figure 5 to illustrate the principles in this tutorial. Figure 5 compares performance between the single-hue color scheme and rainbow color scheme. Figure 5A has low bias but some scatter (moderate precision) across the gray line, which denotes the 1:1 accuracy between true and estimated values. However, Figure 5B has high bias but very little scatter (high precision) due to the easy identification of the groups. Whereas, there was some uncertainty in correctly identifying the true value within each group.

Summary

When deciding on the color scheme for your data, take into consideration what is more important. Is it critical that your audience precisely distinguish one group from another? Or is it more important to have them visually identify the correct value associated with the color? Ideally, you want to be able to use a color scheme that has low bias and high precision, but in reality, you will need to make a tradeoff between the two.

References

I used the following references to develop this tutorial.

Liu Y, Heer J. Somewhere over the rainbow: An empirical assessment of quantitative colormaps. ACM Human Factors in Computing Systems (CHI) 2018, April 21-26, 2018, Montreal, QC, Canada. http://dx.doi.org/10.1145/3173574.3174172

Cromwell W. Colour schemes in data visualisation: Bias and Precision. Presented at the useR! 2016 international R User conference, June 15, 2017. URL: https://channel9.msdn.com/Events/useR-international-R-User-conference/useR2016/Colour-schemes-in-data-visualisation-Bias-and-Precision

Understanding the potential risks and opportunities with naloxone

I wrote a piece for "Incremental Thoughts," the UW Comparative Health Outcomes, Policy, & Economics (CHOICE) Institute blog, about the moral hazard of naloxone access.

The piece is located here.

Generating Survival Curves from Study Data: An Application for Markov Models (Part 2 of 2)

BACKGROUND

In a previous blog, we provided instructions on how to generate the Weibull curve parameters (λ and γ) from an existing Kaplan-Meier curve. The Weibull parameters will allow you to generate survival curves for cost-effectiveness analysis. In the second part of this tutorial, we will take you through the process of incorporating these Weibull parameters to simulate survival using a simple three-state Markov model. Finally, we’ll show how to extrapolate the survival curve to go beyond the time frame of the Kaplan-Meier curve so that you can perform cost-effectiveness analysis across a lifetime horizon.

In this tutorial, I will:

• Describe how to incorporate the Weibull parameters into a Markov model

• Compare the survival probability of the Markov model to the reference Kaplan-Meier curve to validate the method and catch any errors

• Extrapolate the survival curve across a lifetime horizon

Link to the Markov model used in this tutorial can be found here.

MOTIVATING EXAMPLE

We will use a three-state Markov model to illustrate how to incorporate the Weibull parameters and generate a survival curve (Figure 1).

Figure 1. Markov model.

To simulate a Markov model using 40-time units (e.g., months), you will need to think about the different transition probabilities. Figure 2 lists the different transition probabilities and their calculations. We made the assumption that the transition from the Healthy state to the Sick state was 20% across all time points.

Figure 2. Transition probabilities for all health states and associated calculations.

The variable pDeath(t) denotes the probability of mortality as a function of time. Since we have the lambda (λ=0.002433593) and gamma (γ=1.722273465) Weibull parameters, we can generate the Weibull curve using Excel. Figure 3 illustrates how I set up the Markov model in Excel. I used the following equation to estimate the pDeath(t):

where t_i  is some time point at i. This expression can be written in Excel as (assuming T=1 and T+1 = 2):

= 1 – EXP(lambda*(T^gamma – (T+1)^gamma))

Figure 3. Calculating the probability of mortality as a function of time in Excel.

You can estimate the probability of survival as a function of time S(t) by subtracting pDeath(t) from 1. Once you have these values, you can compare how well your Markov model was able to simulate the survival compared to the observed Kaplan-Meier curve (Figure 4).

Figure 4. Survival curve comparison between the Markov model and Kaplan-Meier curve.

View fullsize

Once we are comfortable with the simulated survival curve, we can extrapolate the survival probability beyond the limits of the Kaplan-Meier curve. To do this, we will need to go beyond the reference Kaplan-Meier’s time period of 40 months. In Figure 5, I extended the time cycle (denoted as Time) from 40 to 100 (truncated at 59 months).

Figure 5 illustrates the Weibull distribution extrapolated out to an entire cohort’s life time in the Markov model (Figure 5 is truncated at 59 months to fit this into the tutorial).

Figure 6 provides an illustration of the lifetime survival of the cohort after extrapolating the time period from 40 months to 100 months. The survival curve does a relative good job of modeling the Kaplan-Meier curve. As the time period extends beyond 40 months, the Weibull curve will exponentially reach a point where all subjects will enter the Death state. This is reflected in the flat part of the Weibull curve at the late part of the time period.

Figure 6. Lifetime survival of the cohort using the Weibull extrapolation.

View fullsize

SUMMARY

After extrapolating the survival curve beyond the reference Kaplan-Meier curve limit of 40 months, you can estimate the lifetime horizon for a cohort of patients using a Markov model. This method is very useful when simulating chronic diseases. However, it is always good practice to calibrate your survival curves with the most recent data on the population of interest.

The U.S. National Center for Health Statistics has life tables that you can use to estimate the life expectancy of the general population, which you can compare to your simulated cohort. Moreover, if you want to compare your simulated cohort’s survival performance to a reference specific to your chronic disease cohort, you can search the literature for previously published registry data or epidemiology studies. Using existing studies as a reference will allow you to make adjustments to your survival curves that will give them credibility and validation to your cost-effectiveness analysis.

CONCLUSIONS

Using the Kaplan-Meier curves from published sources can help you to generate your own time-varying survival curves for use in a Markov model. Using the Hoyle and Henley’s Excel template to generate the survival probabilities, which are then used in an R script to generate the lambda and gamma parameters, provides a powerful tool to integrate Weibull parameters into a Markov model. Moreover, we can take advantage of the Weibull distribution to extrapolate the survival probability over the cohort’s lifetime giving us the ability to model lifetime horizons.

The Excel template developed by Hoyle and Henley generates other parameters that can be used in probabilistic sensitivity analysis like the Cholesky decomposition matrix, which will be discuss in a later blog.

REFERENCES

Location of Excel spreadsheet developed by Hoyle and Henley (Update 02/17/2019: I learned that Martin Hoyle is not hosting this on his Exeter site due to a recent change in his academic appointment. For those interested in getting access to the Excel spreadsheet used in this blog, please download it at this link).

Location of the Markov model used in this exercise is available in the following link:

https://www.dropbox.com/sh/ztbifx3841xzfw9/AAAby7qYLjGn8ZfbduJmAsVva?dl=0

Symmetry Solutions. “Engauge Digitizer—Convert Images into Useable Data.” Available at the following url: https://www.youtube.com/watch?v=EZTlyXZcRxI

Engauge Digitizer: Mark Mitchell, Baurzhan Muftakhidinov and Tobias Winchen et al, "Engauge Digitizer Software." Webpage: http://markummitchell.github.io/engauge-digitizer [Last Accessed: February 3, 2018].

1. Hoyle MW, Henley W. Improved curve fits to summary survival data: application to economic evaluation of health technologies. BMC Med Res Methodol 2011;11:139.

 

ACKNOWLEDGMENTS

I want to thank Solomon J. Lubinga for helping me with my first attempt to use Weibull curves in a cost-effectiveness analysis. His deep understanding and patient tutelage are characteristics that I aspire to. I also want to thank Elizabeth D. Brouwer for her comments and edits, which have improved the readability and flow of this blog. Additionally, I want to thank my doctoral dissertation chair, Beth Devine, for her edits and mentorship.

Generating Survival Curves from Study Data: An Application for Markov Models (Part 1 of 2)

BACKGROUND

In cost-effectiveness analysis (CEA), a life-time horizon is commonly used to simulate a chronic disease. Data for mortality are normally derived from survival curves or Kaplan-Meier curves published in clinical trials. However, these Kaplan-Meier curves may only provide survival data up to a few months to a few years. Extrapolation to a lifetime horizon is possible using a series of methods based on parametric survival models (e.g., Weibull, exponential); but performing these projections can be challenging without the appropriate data and software.

This blog provides a practical, step-by-step tutorial to estimate a parameter method (Weibull) from a survival function for use in CEA models. Specifically, I will describe how to:

• Capture the coordinates of a published Kaplan-Meier curve and export the results into a *.CSV file

• Estimate the survival function based on the coordinates from the previous step using a pre-built template

• Generate a Weibull curve that closely resembles the survival function and whose parameters can be easily incorporated into a simple three-state Markov model

 

MOTIVATING EXAMPLE

We will use an example dataset from Stata’s data library. (You can use any published Kaplan-Meier curve. I use Stata's data library for convenience.) Open Stata and enter the following in the command line:

use http://www.stata-press.com/data/r15/drug2b
sts graph, by(drug) risktable

You should get a Kaplan-Meier curve that illustrates the survival probability of two different drugs (Figure 1). The Y-axis denotes the survival probability and the X-axis denotes the time in months. Below the figure is the number at risk for the two drug comparators. We will need this to generate our Weibull curves. (If possible, find a Kaplan-Meier curve with the number at risk. It will make the Weibull curve generation easier.) Alternative methods exist to use Kaplan-Meier curves without the number at risk, but they will not be discussed in this tutorial.

Figure 1. Kaplan-Meier curve.

You will need to download the “Engauge Digitizer” application to convert this Kaplan-Meier curve into a *.CSV file with the appropriate data points. This will help you to develop an accurate survival curve based on the Kaplan-Meier curve. You can download the “Engauge Digitizer” application here: https://markummitchell.github.io/engauge-digitizer/

After you download “Engauge Digitizer,” open it and import the Kaplan-Meier file. Your interface should look like the following:

Figure 2. Engauge Digitizer interface.

The right panel guides you in digitizing your Kaplan-Meier figure. Follow this guide carefully. I will not go into how to use “Engauge Digitizer;” however a YouTube video tutorial to use Engauge Digitizer was developed by Symmetry Solutions and is available here.

We will use the top Kaplan-Meier curve (which is highlighted with blue crosshairs in Figure 3) to generate our Weibull curves.

Figure 3. Select the top curve to digitize.

After you digitize the figure, you will export the data as a *.CSV file. The *.CSV file should have two columns corresponding to the X- and Y-axes of the Kaplan-Meier figure. Figure 4 has the X values end at row 20 to fit onto the page, but this extends till the end of the Kaplan-Meier time period, which is 40.

Figure 4. *.CSV file generated from the Kaplan-Meier curve (truncated to fit onto this page).

I usually superimpose the “Engauge Digitizer” results with the actual Kaplan-Meier figure to prove to myself (and others) that the curves are exactly the same (Figure 5). This is a good practice to convince yourself that your digitized data properly reflects the Kaplan-Meier curve from the study.

Figure 5. Kaplan-Meier curve superimposed on top of the Engauge Digitizer curve.

Now, that we have the digitized version of the Kaplan-Meier, we need to format the data to import into the Weibull curve generator. Hoyle and Henley wrote a paper that explains their methods for using the results from the digitizer to generate Weibull curves.[1] We will use the Excel template they developed in order to generate the relevant Weibull curve parameters. (The link to the Excel template is provided at the end of this tutorial.)

I always format the data to match the Excel template developed by Hoyle and Henley. The blue box indicates the number at risk at the time points denoted by Figure 1 and the red box highlights the evenly spaced time intervals that I estimated (Figure 6).

Figure 6. Setting up your data using the template from Hoyle and Henley.

In order to find the survival probability at each “Start time” listed in the Excel template by Hoyle and Henley, linear interpolation is used. [You can use other methods to estimate the survival probability between each time points given the data on Figure 3 (e.g., last observation carried forward); however, I prefer to use linear interpolation.] In Figure 7, the survival probabilities (Y) correspond to a time (X) that was generated by the digitizer. Now, we want to find the Y value corresponding to the X values on the Excel template.

Figure 7. Generating the Y-values using linear interpolation.

Figure 8 illustrates how we apply the linear interpolation to estimate the Y value that corresponds with the X values from the Excel template developed by Hoyle and Henley. For example, if you were interested in finding the Y value at X = 10, the you would need to input the following into the linear interpolation equation using the following expression:

This yields a Y value of 0.866993, which is approximately 0.87.

Figure 8. Y values are generated using linear interpolation.

After generating the Y values corresponding to the Start time from Figure 5, you can enter them into the Excel template by Hoyle and Henley (Figure 9). Figure 9 illustrates the inputted survival probabilities into the Excel template.

Figure 9. Survival probabilities are entered after estimating them from linear interpolation.

After the “Empirical survival probability S(t)” is populated, you will need to go to the “R Data” worksheet in the Excel template and save this data as a *.CSV file. In this example, I saved the data as “example_data.csv” (Figure 10).

Figure 10. Data is saved as “example_data.csv.”

Then I used the following R code to estimate the Weibull parameters. This R code is located in the “Curve fitting ‘R’ code” in the Excel templated developed by Hoyle and Henley. (I modified the R code written by Hoyle and Henley to allow for a *.CSV file import.)

rm(list=ls(all=TRUE))   
library(survival)   

#    Step 4.   Update directory name and text file name in line below   
setwd("insert the folder path where the data is stored")
data<- read.csv("example_data.csv")
attach(data)
data    

times_start <-c(  rep(start_time_censor, n_censors), rep(start_time_event, n_events) )  
times_end <-c(  rep(end_time_censor, n_censors), rep(end_time_event, n_events)  )   

#  adding times for patients at risk at last time point 
######code does not apply because 0 at risk at last time point  
######code does not apply because 0 at risk at last time point  

#   Step 5. choose one of these function forms   (WEIBULL was chosen for the example)
model <- survreg(Surv(times_start, times_end, type="interval2")~1, dist="exponential")   # Exponential function, interval censoring 
model <- survreg(Surv(times_start, times_end, type="interval2")~1, dist="weibull")   # Weibull function, interval censoring 
model <- survreg(Surv(times_start, times_end, type="interval2")~1, dist="logistic")   # Logistic function, interval censoring   
model <- survreg(Surv(times_start, times_end, type="interval2")~1, dist="lognormal")   # Lognormal function, interval censoring 
model <- survreg(Surv(times_start, times_end, type="interval2")~1, dist="loglogistic")   # Loglogistic function, interval censoring 

#   Compare AIC values  
n_patients <- sum(n_events) +  sum(n_censors)   
-2*summary(model)$loglik[1] + 1*2   #  AIC for exponential distribution 
-2*summary(model)$loglik[1] + 1*log(n_patients)   #  BIC exponential    
-2*summary(model)$loglik[1] + 2*2   #  AIC for 2-parameter distributions    
-2*summary(model)$loglik[1] + 2*log(n_patients)   #  BIC for 2-parameter distributions  


intercept <- summary(model)$table[1]   # intercept parameter    
log_scale <- summary(model)$table[2]   # log scale parameter    

#  output for the example of the Weibull distribution   
lambda <- 1/ (exp(intercept))^ (1/exp(log_scale))    # l for Weibull, where S(t) = exp(-lt^g)   
gamma <- 1/exp(log_scale)     # g for Weibull, where S(t) = exp(-lt^g)  
(1/lambda)^(1/gamma) * gamma(1+1/gamma)    # mean time for Weibull distrubtion  


#  For the Probabilistic Sensitivity Analysis, we need the Cholesky matrix, which captures the variance and covariance of parameters    
t(chol(summary(model)$var))    #  Cholesky matrix   

#  Simulate variability of mean for Weibull 
library(MASS)   

simulations <- 10000  # number of simulations for standard deviation of mean    
sim_parameters <- mvrnorm(n=simulations, summary(model)$table[,1],  summary(model)$var  )   # simulates simulations from multivariate normal    
intercepts <- sim_parameters[,1]   # intercept parameters   
log_scales <- sim_parameters[,2]   # log scale parameters   
lambdas <- 1/ (exp(intercepts))^ (1/exp(log_scales))    # l for Weibull, where S(t) = exp(-lt^g)    
gammas <- 1/exp(log_scales)     # g for Weibull, where S(t) = exp(-lt^g)    
means <- (1/lambdas)^(1/gammas) * gamma(1+1/gammas)    # mean times for Weibull distrubtion 
sd(means)   # standard deviation of mean survival   

# consider adding this (from Arman Oct 2016) to plot KM 
km <- survfit(Surv(times_start, times_end, type="interval2")~ 1)    
summary(km) 
plot(km, xmax=600, xlab="Time (Days)", ylab="Survival Probability") 

There are several elements generated by the above R code that you need to record, including the intercept and log-scale:  

> intercept
[1] 3.494443
> log_scale
[1] -0.5436452

Once you have this, input them into the Excel template sheet titled “Number events & censored,” which is the same sheet you used to generate the survival probabilities after entering the data from the “Engauge Digitizer.” Figure 11 illustrates where these parameters are entered (red square).

Figure 11. Enter the intercept and log scale parameters into the Excel template developed by Hoyle and Henley.

You can check the fit of the Weibull curve to the observed Kaplan-Meier curve in the tab “Kaplan-Meier.” Figure 12 illustrates the Weibull fit’s approximation of the observed Kaplan-Meier curve.

Figure 12. Weibull fit (red curve) of the observed Kaplan-Meier curve (blue line).

From Figure 11, we also have the lambda (λ=0.002433593) and gamma (γ=1.722273465) parameters which we’ll use to simulate survival using a Markov model.

 

SUMMARY

In the next blog, we will discuss how to use the Weibull parameters to generate a survival curve using a Markov model. Additionally, we will learn how to extrapolate the survival curve beyond the time period used to generate the Weibull parameters for cost-effectiveness studies that use a lifetime horizon.

 

REFERENCES

Location of Excel spreadsheet developed by Hoyle and Henley (Update 02/17/2019: I learned that Martin Hoyle is not hosting this on his Exeter site due to a recent change in his academic appointment. For those interested in getting access to the Excel spreadsheet used in this blog, please download it at this link).

Update: 12 January 2023 - The old link to the YouTube video on Engauge was broken. A new link was identified that provided the same content on how to use Engauge.

Location of the Markov model used in this exercise is available in the following link:

https://www.dropbox.com/sh/ztbifx3841xzfw9/AAAby7qYLjGn8ZfbduJmAsVva?dl=0

Design with Greg. “Engauge: A Free Tool for Engineering that pairs great with Excel.” Available at the following url: https://www.youtube.com/watch?v=i1bEFovvvbM

Engauge Digitizer: Mark Mitchell, Baurzhan Muftakhidinov and Tobias Winchen et al, "Engauge Digitizer Software." Webpage: http://markummitchell.github.io/engauge-digitizer [Last Accessed: February 3, 2018].

1. Hoyle MW, Henley W. Improved curve fits to summary survival data: application to economic evaluation of health technologies. BMC Med Res Methodol 2011;11:139.

ACKNOWLEDGMENTS

I want to thank Solomon J. Lubinga for helping me with my first attempt to use Weibull curves in a cost-effectiveness analysis. His deep understanding and patient tutelage are characteristics that I aspire to. I also want to thank Elizabeth D. Brouwer for her comments and edits, which have improved the readability and flow of this blog. Additionally, I want to thank my doctoral dissertation chair, Beth Devine, for her edits and mentorship.

Counting and Data Manipulation for an ITSA

BACKGROUND

In time series analysis, we are interested on the impact of some exposure over a time period. Exposure can be coded as event==1. If this is time-varying, then the event can occur at any time across a time period. Time series analysis requires us to identify the time when the event first occurred. In most cases this is also considered the post period. In this example, we will label the exposure of interest as event.

Longitudinal data can come in either a wide or long format. However, it is easier to perform longitudinal data analysis in the long format. This assumes that you declare either the xtset or tsset as a panel or time-series data set, respectively.

MOTIVATING EXAMPLE

Let’s assume that we have two subjects (A and B), who can experience an event at any time between some time variable 1 and 5, time(1:5). This is a longitudinal data set in the long format with id as the unique subject-level identifier, the exposure variable of interest event as the exposure, and time as an arbitrary time variable ranging from 1 to 5. The event for subject A occurs at time==3.

Suppose you want to create a variable that counts the number of times the subject has the event. We will call this variable duration.

The following Stata code will generate the duration variable.

by id (time), sort: gen byte duration = sum(event==1)

Sorting by the id and then time will nest the time sequence for each id. The sum() will add all event that is coded as 1.

It’s critical that you put time in parentheses (); otherwise, you can generate incorrect values. For instance, if you make the mistake of typing the Stata code as follows, you will generate a dataset which doesn’t provide the cumulative duration of having the event. Notice how the duration variable only has 1 instead of 1, 2, and 3.

by id time, sort: gen byte duration = sum(event==1)

Similarly, if you use the following code, you will generate the incorrect values. The sum(event)==1 syntax should be sum(event==1). However, this will “flag” the time when the event first occurred, which may be useful in some cases. 

by id (time), sort: gen byte duration = sum(event)==1

Let’s take our example further and generate a variable column that takes into consideration the period before the subject experiences an event. Suppose subject A experiences an event at time==3, but we want to center this as 0 and previous months as -1, -2, and so on. We need to first identify the time when the event occurs and populate that as a new variable, which we will call firstevent. We can use the following State code to generate firstevent based on the condition that the event==1 and the variable it occurs is time==3.

egen firstevent = min(cond(event == 1, time, .)), by(id)

There will be missing values since not all subjects experience the event. To populate the missing values for the subjects with no events (event==0), we need to replace firstevent by identifying the max time of the entire study period using the summary command. Once we have the max time of the study period, we add 1 to this and replace the missing values from the firstevent variable.

replace firstevent = max(time) if firstevent == .
summ time
global maxtime = r(max)

replace firstevent = $maxtime + 1 if firstevent == .

We can subtract the time from the first event to generate a new variable (its) that will capture the negative time before the event occurs and the positive time after the event occurs, centered on when event==1.

by id (time), sort: gen byte its = _n – firstevent

The new variable its is short for interrupted time series analysis. An investigator can use the its variable to plan any interrupted times series analysis without having to go through the ordeal of generating this variable using other software.

Here is a summary of the entire Stata code, which you can also find on my Github page:

***** Declare XTSET panel dataset.
* Variable list: id event time 
* id        =   subject identifier
* event     =   exposure of interest
* time      =   time interval

**** Create the duration variable to capture time after event.
by id (time), sort: gen byte duration = sum(event==1)

**** Create a variable for the time before the event.
egen firstevent = min(cond(event == 1, time, .)), by(id)

**** Identify the maxtime.
summ time
global maxtime = r(max)

**** Replace missing data with the maxtime + 1.
replace firstevent = $maxtime + 1 if firstevent == .

**** Create its to capture time before and after event. 
by id (time), sort: gen byte its = _n - firstevent

ACKNOWLEDGEMENTS

I used several online references to develop this tutorial for Stata. Nicholas J. Cox has some excellent tutorials that was influential in developing this piece.

Cox N. First and last occurrences in panel data. From https://www.stata.com/support/faqs/data-management/first-and-last-occurrences/

The Statlist forum was also helpful; in particular, the following discussion threads.

https://www.statalist.org/forums/forum/general-stata-discussion/general/965910-how-generate-variable-that-indicates-current-and-prior-event-occurrence-for-id-in-panel-data

https://www.statalist.org/forums/forum/general-stata-discussion/general/1297707-creating-duration-variable-for-panel-data

https://www.stata.com/statalist/archive/2010-12/msg00193.html

https://www.stata.com/statalist/archive/2012-09/msg00286.html

The UCLA Institute for Digital Research and Education has a tutorial on using _N and _n to count in Stata.

Counting from _N to _N. UCLA: Statistical Consulting Group. From https://stats.idre.ucla.edu/stata/seminars/notes/counting-from-_n-to-_n/

Excel macro to convert cell values in a pivot table from COUNT to SUM

Background

I was preparing a report for the Veterans Health Administration and I ran into an inconvenience where I had to convert the values in a pivot table from the default COUNT to SUM. Normally, this would not be an onerous process. However, there were several columns that I wanted to convert, which would take an enormous amount of work to perform. Fortunately, I ran into Doctor Moxie's blog, which providers tips and tricks to using Excel efficiently. You can find the blog here.

Doctor Moxie created a Visual Basic Macro that conveniently converts all the data in the pivot table from the default COUNT to SUM.

Motivating Example

To illustrate the solution, I used the following example dataset, which was generated using the following function:

=RANDBETWEEN(0, 100)

This will generate a value between 1 and 100 for each cell.

I used the pivot table to see see the number of hours per region. From the pivot table, the values were reported as COUNT per region instead of SUM per region.

I could go through each column and change the values from COUNT to SUM, but this would be inconvenient if there were over 100 columns.

Doctor Moxie developed an inventive solution to address this problem using a macro, which you can get from his/her website.

Using the macro converted the values from COUNT to SUM.

The macro nicely converts all the cells and makes the analysis easier to perform. This saved me hours of work and I recommend you keep this macro in your Excel arsenal.

Acknowledgements

Doctor Moxie is credited with developing the macro and his/her website (ExcelPivots) can be found here.

Communicating data effectively with data visualization - Part 4 (Time series)

Introduction

An important element of data visualization is to tell a story. To do that, we should have the end in mind. Namely, what is it you want to share with your audience?

Often, time series data can do this using some clever data visualization. Typically, this is presented on an XY plane where time is presented on the X-axis and the value of interest is presented on the Y-axis. We will not go into time series analysis, which involves a lot more than just plotting the data. However, we will go over the proper way in which to present your time series data visually.

Motivating example

We will use data from the National Health Expenditure Account (NHEA), which contains historical data on health expenditures in the U.S. from 1960 to 2016. The costs presented by the NHEA are properly adjusted for inflation. You can find the data at this link: https://www.cms.gov/Research-Statistics-Data-and-Systems/Statistics-Trends-and-Reports/NationalHealthExpendData/NationalHealthAccountsHistorical.html

Time series data

To visualize time series data, it is best to have increments of time that are equally spaced in the X-axis. We use Excel to illustrate these examples. Figure 1 illustrates the annual interval of national health expenditures ($ billions) in the United States from 1960 to 2016. The outcome (national health expenditure) is on the Y-axis and time (year) is on the X-axis. Notice that each time increment is one year and evenly spaced across the X-axis. This allows the eyes to intuitively see the changes across time in the U.S. national health expenditure.

Figure 1. National Healthcare Expenditure in the United States, 1960 to 2016.

What if the story is to see highlight health expenditures in the last decade? How would we do this?

First, we can use the same data and restrict the X-axis to 2007 to 2016 as in Figure 2.

Figure 2. National Health Expenditures in the United States, 2007 to 2016.

Figure 2 doesn’t seem interesting. There is an increase in health expenditures from 2007 to 2016, but this doesn’t seem significant. However, there is a 45% increase from 2007 to 2016 in health expenditures ($2,295 billion to $3,337 billion). Figure 2 doesn’t convey this increase because there is a lot of white space between the lowest health expenditure value in 2007 and $0.

One way to illustrate the large increase in health expenditure is to truncate the Y-axis. In previous articles, we stressed that truncated axis can distort and trick the mind into seeing large differences where they don’t exist. However, this same technique can be used to make sure that differences that exist are not misinterpreted as not visually significant. According to Tufte:

In general, in a time-series, use a baseline that shows the data not the zero point. If the zero point reasonably occurs in plotting the data, fine. But don't spend a lot of empty vertical space trying to reach down to the zero point at the cost of hiding what is going on in the data line itself.[1]

In other words, time series data should focus on the area of the timeline that is interesting. The graphic should eliminate the white space and show the data horizontally for time series visuals.

Eliminating the white space and identifying the baseline value as $2,200 billion instead of $0 changes the figure as illustrated in Figure 3.

Figure 3. National Health Expenditures in the United States, 2007 to 2016.

Figure 3 illustrates the increase in national expenditure in the last decade better than Figure 2 and maintains the narrative that there was a visually significant increase.

Putting these concepts together (along with Tufte’s other principles), we can generate a similar figure using R (Figure 4). The R code is listed below.

# Plot trend - without truncation
library(lattice)
  
xyplot(y~x, 
       xlab=list(label="Year", cex=1.25),
       ylab=list(label="National Health Expenditures ($ Billions)", cex=1.25),
       main=list(lable="National Health Expenditure (2007 to 2016)", cex=2),
       par.settings = list(axis.line = list(col="transparent")),
       panel = function(x, y,...) { 
          panel.xyplot(x, y, col="darkblue", pch=16, cex=2, type="o")
          panel.rug(x, y, col=1, x.units = rep("snpc", 2), y.units = rep("snpc", 2), ...)})

Figure 4. National Health Expenditures in the United States, 2007 to 2016.

Figure 4 incorporates the use of Tufte’s principles on data-ink ratio and truncation on the y-axis to highlight the change in National Health Expenditure between 2006 go 2017.

Conclusions

With time series data, truncating the Y-axis to eliminate white space and show the data horizontally is appropriate when telling the story of what’s happening across time. Using zero as the baseline for the Y-axis is appropriate if it is reasonable. However, do not compromise the story by having the Y-axis extend all the way to zero if it doesn’t tell the story properly. Knowing when and how to truncate the Y-axis will help you explain to your audience the significance of a change across a specific period in time.

References

1. Edward Tufte forum: baseline for amount scale [Internet]. [cited 2018 Jan 14];Available from: https://www.edwardtufte.com/bboard/q-and-a-fetch-msg?msg_id=00003q

Communicating data effectively with data visualization – Part 3 (Truncated Axis and Area as Quantity)

Introduction

Data visualization is a powerful tool that allows us to use data to tell an engaging story. The narrative we present is enhanced by our data, especially when it is easily accessible and intuitive to understand. This is evident by the large amount of data visualization tools and galleries available throughout the internet. For example, Tableau Software hosts a data viz gallery that allows users to post their creations using their software. However, for most users, Microsoft Excel is the first tool they are exposed to when it comes to developing data visualizations for their business, school, and social projects.

Creating data visualization has its caveats. Improper data visualization can mislead, distort, and “lie,” which can result in poor decisions, loss of profit, and regret. In this blog, we will explore two of the most common distortion techniques that violate Tufte’s principles of graphical integrity: Truncated Axis and Area as Quantity.[1]

 

Motivating example

We will use data from the Medical Expenditures Panel Survey, which is a large-scale survey of households on health care resource use and spending in the United States. We will compare insurance status (Private, Public, Uninsured) between genders, which is summarized in Table 1. We will use Microsoft Excel to generate all our examples.

 

Distortions

Data visualization has opened the door to increased misrepresentation of numbers. Interest groups and advocates will distort the data visualization to try and mislead or convince their audience of their arguments or narrative. Such techniques include using truncating axes and disproportionate sizes.

Let’s compare the difference in the proportion of males with public insurance to females with public insurance. In Figure 1, a bar chart is used to compare the proportion of males and females with access to public insurance. In Panel A, a truncated y-axis is used to distort the difference in the proportion of males and females with public insurance. The absolute difference is approximately 4%. However, Panel B, which uses a non-truncated y-axis, the perceived difference is not as great as that appearing in Panel A, despite having an absolute difference of 4%. Our mind perceives Panel A as having a greater difference; however, Panel B shows the same absolute difference of 4%, but does not illicit the same perception. This is supported by a study performed by Pandey and colleagues who reported that respondents rated the truncated bar chart as having a greater difference than the non-truncated bar chart.[2] It is our recommendation that a non-truncated y-axis is used when presenting data as a bar chart.

Figure 1. Comparisons of bar charts using a truncated y-axis (A) and a full y-axis (B).

Another distortion technique uses disproportionate sizes or “Area and Quantity” method. With this distortion, the values or quantitative data is not proportional to the area that represents it. Tufte argues that “the representation of numbers, as physically measured on the surface of the graph itself, should be directly proportional to the numerical quantities represented.”[1] In order words, the area used to represent the values or quantitative data should not be grossly exaggerated. Figure 2 illustrates how this principle is violated.

Figure 2. Proportion of males and females with public insurance using improper Area as Quantity.

In Figure 2, 27% of males have public insurance versus 31% of females. In terms of relative difference, females have a 15% greater proportion with public insurance compared to males per the equation: .

However, the area in Figure 2 has females with an area that is 96% greater than males, which is not reflective of the relative difference of 15%.

Figure 3 illustrates the correct Area as Quantity that reflect the relative difference between males and females with public insurance. We estimated the area of the circle for males and females and properly adjusted the sizes to reflect their relative differences. Now, the relative difference is not as great as previously illustrated. Instead, we have an accurate representation of the relative difference in having public insurance between males and females. We recommend estimated the area of a shape to reflect the relative difference between the groups with these types of data visualizations.

Figure 3. Proportion of males and females with public insurance using the proper Area as Quantity.

Conclusions

Distortions can mislead or convince an audience of a narrative that do not reflect the actual data. Developing data visualization that provides empirical support for your narrative should be accurate and honest. Fortunately, innocent mistakes like the examples above are easy to correct, especially when using programs like Microsoft Excel.

 

Notes

We calculated the area of the circle using Archimedes method where Area = pr^2 where p is the constant (p=3.14) and r is the radius of the circle.

 

References

1. Tufte ER. The Visual Display of Quantitative Information. Second. Cheshire, CT: Graphics Press, LLC.; 2001.

2. Pandey AV, Rall K, Satterthwaite ML, Nov O, Bertini E. How Deceptive Are Deceptive Visualizations?: An Empirical Analysis of Common Distortion Techniques [Internet]. In: Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems. New York, NY, USA: ACM; 2015. p. 1469–1478.Available from: http://doi.acm.org/10.1145/2702123.2702608

Communicating data effectively with data visualization – Part 2 (Distortions, Scales, and Volume)

Introduction

It is tempting to “enhance” our data visuals in order to “spice-up” the narrative. Changing perspective, scale, and using unreasonable comparisons can “trick” the mind into thinking that an effect is real when it isn’t. Of course, a reasonable amount of creativity is needed in the narrative, it is important to consider what your best options are. According to Edward Tufte, the pioneer of data visualization, number (values) should be directly proportion to the numerical quantities represented. The graphic should not inflate the actual magnitude of that change. Moreover, Tufte also stated that our data visualization should avoid graphical distortions and ambiguity. Data should be shown in context and properly labelled to avoid ambiguity. Most importantly, we should avoid using “chart junk.”  

Goals

In this blog, we will use data from the Washington State Department of Health Adverse Event Report from 2016 to illustrate concepts of visual distortions, scales, and volume in designing your data visualization.

Motivating example

The Washington State Department of Health provides quarterly reports of serious adverse events that occur across 94 Acute Care Hospitals, 186 Ambulatory Surgical Facilities, 18 Child Birthing Centers, 8 Department of Corrections Medical Facilities, and 7 Psychiatric Hospitals. Figure 1 is a 3-dimensional bar chart of the frequency of serious adverse events that occurred in 2016.

Figure 1. Number of adverse events in Washington State (2016).

Excel generates this bar chart by default (we included the y-label title and chart title). There are two pieces of data used to make this bar chart: frequency and type of adverse events. However, this bar chart actually is illustrated in three dimensions. The lack of a third element makes 3-dimensional charts inappropriate. In fact, it doesn’t make sense to have this extra dimension to the bar chart. Figure 2 illustrates this principle. In the first two dimensions, you have data (frequency and type of adverse events) but the third dimension lacks any meaningful data. This is ambiguous and distorts the true meaning of the bar chart. Therefore, it is recommended that the third dimension is removed in favor of a 2-dimensional bar chart.  

Figure 2. Multiple dimensions of data visualization with a bar chart.

Figure 3 removes the unnecessary dimension and presents the frequency of adverse events without any ambiguity. We also remove the gridlines because they are considered a waste of ink that doesn’t provide more information about the data visualization (data-ink ratio).

Figure 3. Bar chart on the number of adverse events in WA state in 2016.

Figure 4 rearranges the types of adverse events in descending order. Ordering the types of serious adverse events in either ascending or descending order helps to see which categories have the most or least amount of adverse effects. Since there is no order in the categories (nominal categorical data), it’s reasonable to order them based by the frequency of events.

Figure 4. Bar chart with the types of adverse events in descending order.

We can add gridlines to the bar chart to better enhance our ability to detect differences in the frequency of adverse events. Figure 5 illustrates the results after gridlines are added to separate counts of the bar chart into intervals of 50, which is easier to synthesize visually.  We also reduced the y-axis maximum limit from 400 to 350 to remove the empty space and increase our data-ink ratio.

Figure 5. Bar chart with gridlines.

Gridlines that overlay in front of the bar charts is not a feature in Excel. All gridlines are in the background (default), which do not achieve the effect in Figure 5. If you turn the gridlines on, you’ll see something similar to Figure 6 where the gridlines are in the background and do not overlay the bars in the chart. To achieve the look in Figure 5, you need to make a few additional modifications to the data and chart.

Figure 6. Bar chart with gridlines turned on.

Here is the setup for our data to include gridlines in front of the bar chart. We used a “5.5” for our x-axis because there are five types of adverse effects and we reserved the next x-axis bin as the location of our scatter plot values. You can always modify this based on the number of categories in the x-axis. Additionally, we chose to use a 50-count interval. 

After selecting the data, Excel will automatically incorporate these data into the current bar chart.

Right-click on the orange bars and change the chart type to scatter plot XY.

The scatter plot values will plot a point on each x-axis value.

Next, right-click on the plot area and click “Select data...” You may need to change the Series 2 data X-axis values to 5.5 by selecting the columns in your data. This is because Excel automatically plots the scatter plot using the x-values from Series1, which contains the data for the frequency of adverse events (not shown). 

When you click the box on the right, you will be prompted to select the data array. Select the left column of the data set and click “Ok.”

You bar chart should look like the following.

Left click on the dots for the scatter plot and the “More Error Bars Options.”

Make sure you are working on the horizontal error bars and select “Minus” for the Directions, “No Cap” for the End Style, and “Custom” for the Error Amount.

Specify a value for the “Negative Error Value” as 5. Then click “Ok.” Your plot should look like the following.

Now, you can change the width of the error bars, change the color of the error bars to white, and hide the scatter plot dots to get the chart in Figure 5. We used a navy blue color for the bars and a width of 1.5 for the error bars and increased by width by 15%.

After making additional changes to the font and color, our final bar chart can impress while yielding very useful information about the number of adverse events in WA state in 2016. You can easily discriminate the most common type of adverse events and quickly eyeball by how much. 

Conclusion

In this blog, we explained the rationale for not using dimensional bar charts with 2-dimensional data. We also provided instructions on how to create bar charts with gridlines that are informative and in front of the bars. In the next blog, we will discuss distortion and how it can generate ambiguity and confusion when not properly scaled.

References

Credit for creating the gridlines in front of the bars goes to Jon Peltier who wrote a tutorial on gridlines (https://peltiertech.com/column-chart-gridlines-cutting-through-bars/).

1.     Tufte ER. (2001) The Visual Display of Quantitative Information. Second Edition. Cheshire, CT. Graphics Press, LLC.

Communicating data effectively with data visualizations - Part 1 (Principles of Data Viz)

Introduction

Data visualization is a form of visual communication that takes quantitative information and displays it as a graphic, an abstraction of the real world. Effective data communication makes complex statistical analysis accessible without excessive mental burden. It is also used to identify patterns through data exploration. Unlike information visualization which includes catch-phrases such as “Infoviz” and “Infographics,” data visualization is intuitive, informative, and “pretty” while simultaneously focused on scientifically structured comparisons, analytic precision, and statistical inference. The challenge is compressing all the quantitative information into a single chart or graphic that provides a narrative or purpose that can be synthesized and acted on with very little mental effort.

There are a variety of data visualizations that can be used such as choropleths, heatmaps, scatter plots, and dot plots (this list is not all inclusive). The selection is dependent on the data, audience, and narrative. How complex is the analysis? Who are you presenting this information to? Why should the audience care?

The best way to present data effectively is with a good story. Your graphic should be able to tell a story based on the quantitative information. Every graphic you create should be a self-contained narrative of the data. This can be achieved using simple tools, but the creation of effective data visualization depends more on your ability to tell a good story. The purpose of this article is to highlight some important principles of data visualization, review common data visualizations, and develop a mechanism to select the most effective data visualization.

Principles of data visualization

Data visualization can be traced to several different schools of thought (e.g., Edward Tufte and William S. Cleveland), but the fundamental principles are similar and often overlap. Edward Tufte identified several key principles when developing data visualizations (Table 1).

Table 1. Tufte's principles for graphical integrity. *
Principle**	Description
Avoid chart junk	Inventive displays seldom generate interest. Rather, they generate visual noise.
Data-ink ratio	Use ink to show the data. Ink that does not contribute to the reporting of the data should be removed.
Numbers should be directly proportional to the numerical quantities represented	The "Lie Factor" is a proportion of the Size of the effect shown in the graphing / Size of the effect in the data. The graphic should not inflate the actual magnitude of the change.
Use small multiples and repeat	High quality information graphic portrays many numbers per square inch. Small multiple, comparative images work especially well for this. Examples include sparklines.
Avoid graphical distortions and ambiguity	Avoid distortions of numbers by graphic devices. Show data variation in context, and label them. Write out explanation of the data on the graphic itself. Properly label events in the data.
Multifunction	Information layers and architecture emerge best when data display elements serve multiple functions. Different readings at different levels of detail (micro-macro) serve this goal well. For example, the y-axis can be used to provide scale while calling out to important values by either coloring that value differently or enlarging it.
Show data variation, not design variation	Use scales that are similar and do not generate ambiguity. Be consistent in the data when displaying them as a graphic.
In time-series displays of money, deflated and standardized units of monetary measurement are nearly always better than nominal units	Properly adjust current due to inflation or population growth. We want to the currency in real purchasing power (value) rather than nominal purchasing power.
The number of information-carrying (variable) dimensions depicted should not exceed the number of dimensions in the data	Using graphics to show the proportional change of a metric can bias our perception due to the number of dimensions that are changing. If we look at a single metric such as budget, then we are only looking at a one-dimensional scale, meaning that when the budget increase, it only changes in one dimension. However, it is easy to use a display such as a 2-dimensional picture and scale it up according to the one-dimensional scale. For example, if we have a 2-dimensional graphic and we scale it according to an increase on a one-dimensional metric, the actual proportional increase in 4 times (2^2 = 4). If this was a 3-dimensional object, then the proportional increase in 8 (2^3 = 8).
Graphics must not quote data out of context	An accurate picture must report the totality of the effect. Showing only one piece of the data with graphics is just as bad as the data. Context is critical. In time-series analysis, it is imperative that the researcher provides an illustration of the overall trend including any changes in seasonality. Therefore, apply rational judgement when presenting data visualization. The use of comparison groups helps to answer any secular impacts that may not be captured when looking at data at a single point in time.

* From Tufte ER. (2001) The Visual Display of Quantitative Information. Second Edition. Cheshire, CT. Graphics Press, LLC.

** This table provides fundamental principles on graphical integrity and data graphics and is not all inclusive.

Figure 1. Box plots of MLB wins in the 2017 season. [click to enlarge]

View fullsize

Dot plots are simple graphics that use points (filled in circles) instead of line or bars on a simple scale. They convey the same information as bar charts, but use less ink to do so. The advantage they provide is that they reduce the junk of the bar charts which contain useless space that are uninformative. In Figure 2a, the dot plot provides the same information from the previous bar charts; however, there is a better sense of scale with the removal of the clutter introduced by the bar charts. Like the bar charts, use pastel colors to dampen the effect of the teams that are not the focus of the chart and use solid colors to bring out the teams with the most and least wins (Figure 2b). The minor grid lines do not provide any information about the data and should be removed (Figure 2c). Finally, Figure 2d takes the dot plots and use data values to provide the audience with the actual number of wins. This is also reinforced by the pastel and solid colors, which provide good contrast between the teams that have the most and least wins.

Figure 2. Dot plots of MLB wins in the 2017 season. [click to enlarge]

View fullsize

Line plots are graphics that use lines to illustrate a trend. A line plot would not be appropriate for the baseball wins example because the x-axis does not have any continuous scale, which is needed for line plots. Table 2 provides data on MLB players’ batting averages from 2013 to 2017. The table provides us with information across five years, but the order and rankings are difficult to determine.

Table 2. Batting averages of Major League Baseball players (2013-2017).
Players	2013	2014	2015	2016	2017
Yasiel Puig	0.319	0.296	0.255	0.263	0.260
Justin Turner	0.280	0.340	0.294	0.275	0.332
Michael Trout	0.323	0.287	0.299	0.315	0.329
Ichiro Suzuki	0.262	0.284	0.229	0.291	0.250

The table doesn’t do a good job illustrating the trends over time. Instead, it is a good reference that is searchable. When it comes to visually telling a story, the table doesn’t do a good job. Converting this table to several line plots can help illustrate the changes in each players’ batting averages over time. Figure 3a trends each player’s batting averages, but the clutter makes it difficult to identify any important patterns. For graphics that use a time interval (or continuous interval) on the x-axis, it is useful to truncate the y-axis to see any incremental changes in the trend.

Figure 3b truncates the batting average from 0 to 0.360 to 0.200 to 0.360. Now the changes in batting average is more discernable from this truncated y-axis. It’s clear that Yasiel Puig’s batting average declined from 2013, but Justin Turner’s batting average improved. However, this still feels cluttered. The different lines and colors make it hard tell that Justin Turner was improving. In fact, it seems like all the players except for Yasiel Puig were improving. To make sense of the clutter, let’s assume that we were interested in the player who had the most improvement from 2013. Calculating the percent change between 2013 and 2017 and then putting it on the graphic provides us with some metric to distinguish Justin Turner from the rest of the other players.

Figure 3c adds the percent change in batting averages from 2013 to 2017 with the player’s name. The legend was removed because it didn’t contribute much to the graphic once the names were adjacent to each line. Despite these modifications, it’s not easy to distinguish the improvement in batting averages for Justin Turner. There are too many competing colors, which distract the focus from Justin Turner’s improvement.

Figure 3d dampens the non-critical lines using a single pastel color and matching the to the trend lines, which highlights Justin Turner’s trend line, the only one with color. This technique draws your attention to Justin Turner’s trend while providing details about the change in trend and the player associated with that change.

Figure 3. Line plots of MLB players’ batting averages (2013-2017). [click to enlarge]

View fullsize

Summary

So far, basic principles and examples of data visualization were presented in this article, which is part of an on-going series on data visualization. Since this is a primer on data visualizations, you should review existing graphics and try to apply some of these principles. Web-based data visualizations are prevalent and can be found in places such as the R-Shiny gallery and Tableau gallery. As you start to explore different data visualizations, you’ll discover many creative and useful tools. Next issue, we’ll discuss other data visualization graphics that will reflect the Tufte’s principles for graphical integrity and excellence.

References

Tufte ER. (2001) The Visual Display of Quantitative Information. Second Edition. Cheshire, CT. Graphics Press, LLC.

Knaflic CN. (2015) Storytelling with Data: A Data Visualization Guide for Business Professionals. Hoboken, New York. John Wiley & Sons, Inc.