Communicating data effectively with data visualization - Part 11 (Waterfall charts)

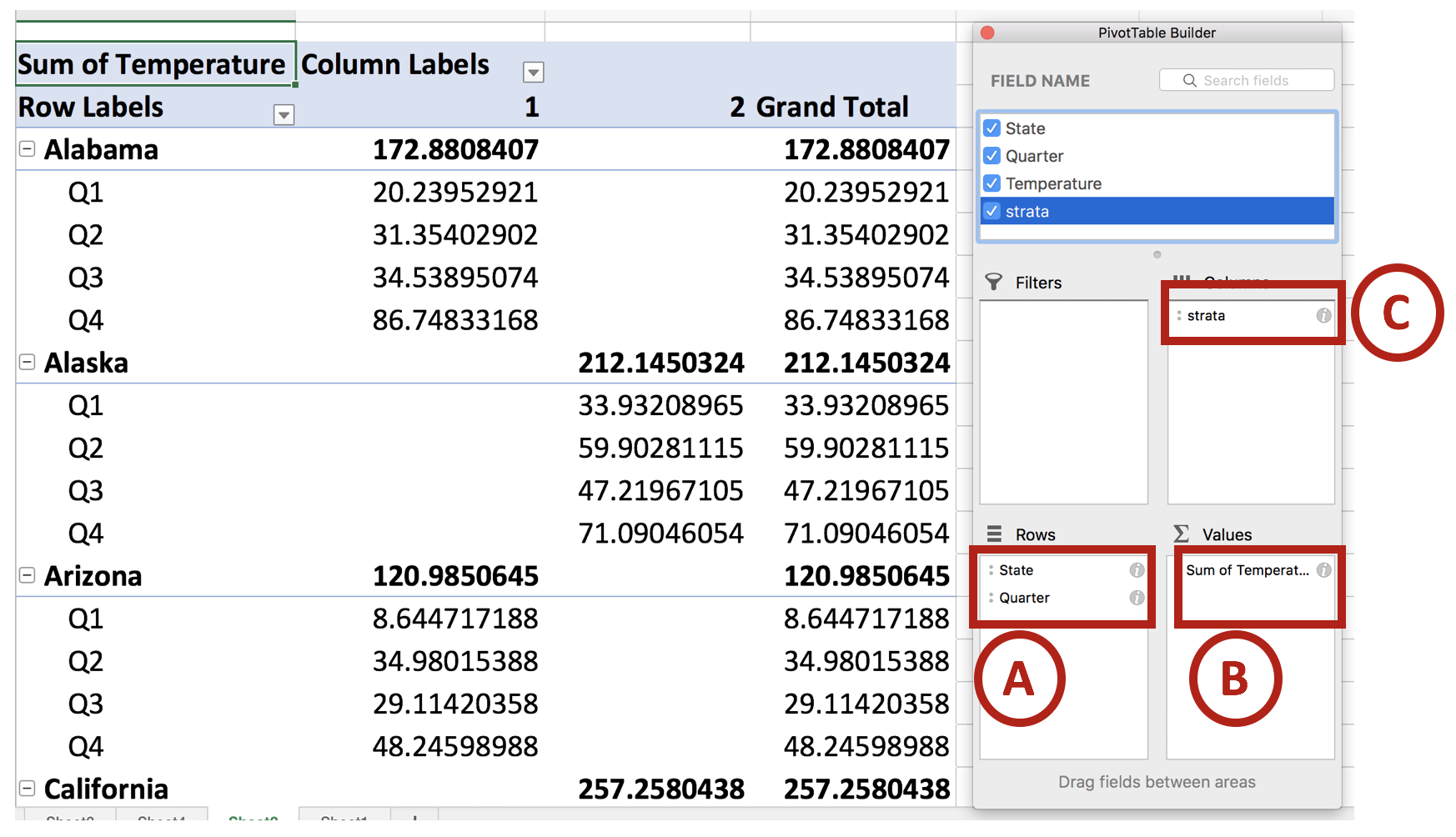
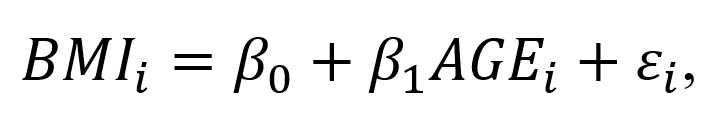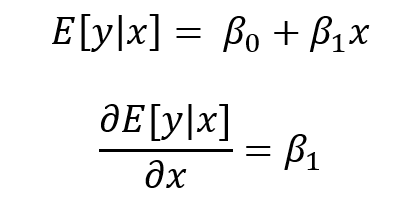BACKGROUND

Changes in data values happens. But when you want to visualize these changes, you need to choose the visualization that best explains the narrative. In this article, we will explore the use of waterfall charts, which are a form of data visualization that illustrates changes from the reference value across some sequentially ordered axis (e.g., time).

MOTIVATING EXAMPLE

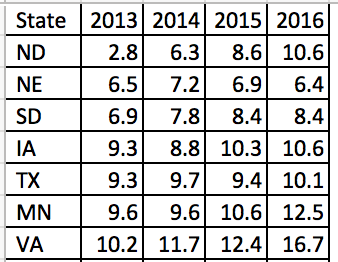
I created a dataset where the average duration of an academic detailing educational outreach visit was estimated from Quarter 1 Fiscal Year 2017 (Q1 FY17) to Quarter 4 Fiscal Year 2018 (Q4 FY18). The initial dataset includes the reference (or base) average duration (in minutes) of an academic detailing educational outreach visit followed by positive and negative changes to the reference value. (Excel example can be retrieved from the following link.)

There are a few things to consider when reviewing this table. The reference value is 25 minutes, which was the average duration in Q1 FY17. However, in Q2 FY17, the average duration decreased by 5 minutes for a new value of 20 minutes. Then in Q3 FY17, the average duration increased by 15 minutes for a net gain of 10 minutes from the reference value of 25 minutes (25 + 10).

Understanding how these values reflect the net gain from the reference value is critical in building the waterfall chart.

TUTORIAL

Step 1: Create three new columns (base, fall, and rise)

We need to do some calculations to generate the base values for the waterfall chart.

Start by creating three additional columns and label them as base, fall, and rise (I learned how to design my table from this YouTube video by United Computers).

 Step 2: Estimate the value for the fall column

For the fall column, we want to look at the Duration column. If the value in the Duration column is positive, then we need to have the value in the “fall” column as zero. If the value in the Duration column is negative, when we want the absolute (positive) value in the “fall” column.  

Here is an illustration of what the “fall” column calculation requires.

Step 2: Estimate the value for the rise column

To estimate the rise column we, again, look to the Duration column. If the value in the Duration column is positive, we enter it into the “rise” column. If the value in the Duration column is negative, then we enter 0 in the “rise” column.

Here is an illustration of what the “rise” column calculation requires.

Step 3: Estimate the value for the base column

The base column provides the necessary reference for us to create the waterfall chart. Unlike the other columns, we start in the base column Q2 FY17 row since the “base” column value in Q1 FY17 is the reference. Then we add the “rise” column in Q1 FY17 and subtract the “fall” column in Q2 FY17. We do this for all the remaining cells.

Here is an illustration of what the “base” column calculation requires.

Step 4: Review the final data

The final data should look like the following.

Step 5: Create a stacked bar chart

Select the data from the Time, base, fall, and rise columns and then insert a stacked bar chart.

You should have a chart that looks like the following.

Step 6: Hide the base stacked bars

The next step is to hide the base column values by selecting the blue bars and changing the formatting to No Fill and No Line.

Step 7: Format the chart for final presentation

You should format the chart using colors that indicate the direction of the rise and fall in the average duration of educational outreach visits. I selected blue for an increase and red for a decrease. I also added the Y-axis label and decreased the gap width to 10%.

Final waterfall chart

CONCLUSIONS

The waterfall chart visualizes the rise and fall in average duration of an academic detailing visit across two fiscal years. This visualization provides the viewer with an intuitive summary of the changes that occurred and whether action plans are needed. From this example, we notice that the changes did not deviate from the base of 25 minutes per visit across two fiscal years. Therefore, there may not be a need to spend resources to investigate this element of academic detailing.

In this example, I re-created the waterfall chart to illustrate seasonal changes.

Like the previous waterfall chart, this is a clear and intuitive visualization of the changes that occurred across two fiscal years. The red bars easily illustrate that the average duration decreased immediately after Q1 FY17, but increased after Q1 FY18 only to follow the same pattern as the previous fiscal year. This tells us that something is going on during Q1 of each fiscal year, which may require some kind of investigation of the program at the beginning of each fiscal year.

Microsoft Office 365 for Windows and Microsoft Office 2016 for the Mac have a new feature for creating waterfall charts. You may need to check the Office Updates to acquire these new features.

You can learn about these in the following Microsoft Office sites (link 1, link 2)

REFERENCES

I used the following YouTube video by United Computers to help generate the waterfall charts in this article.

I also referred to Cole N. Knaflic’s blog on waterfall charts.

Developing choropleths using the United States Veterans Integrated System Network (VISN) shapefiles

BACKGROUND

When I want to present VISN-level data, I consider using choropleths because they are visually appealing and provide a good reference to other VISNs. Choropleths are maps that uses polygons or shapes that are shaded according to a metric such that the color indicates the intensity of that metric. For instance, if you wanted to compare population density across different states, you can use a choropleth to illustrate this difference.

An example of a choropleth comes from the Centers for Disease Control and Prevention that illustrates the prevalence of obesity by state. The legend tells us the prevalence of obesity at each state and the colors denote the level of the prevalence. The cranberry color denotes an obesity prevalence of 35% or greater whereas a lighter green color with dots denotes a prevalence of less than 20%. This choropleth provides a quick visual guide on the prevalence of obesity across the United States (U.S.).

Motivating example

In past reports, I have generated a choropleth using VISN-level data. Unlike the U.S. shapefile (map files with coordinates; normally with the *.shp extension), the VISN shapefile is specific to the VA and doesn’t not follow the borders of the states used in typical U.S. shapefiles.

In this example, I will provide a step by step guide on how you can generate your own VISN-level choropleth for use in reports and presentations. The files for this tutorial are available on following Dropbox link.

TUTORIAL

Step 1: Download QGIS

Download QGIS, which is a free Geographic Information Systems (GIS) software for both the Windows and Mac operating systems. Watch the following video for a step-by-step guide on downloading and using the program. The program is simple to use and does not involve any coding. After you install the software, proceed to the next step. (Contact your local IT support to have this installed on a government-owned system.)

Step 2: Download the VISN shapefiles

The VA provides shapefiles online at the following link. Download the file titled FY2017_Q4_VISN.zip. This file will contain all the necessary files that you will need to build your choropleth.

Step 3: Download VISN-level data on total population

We will need VISN-level data to join with the VISN-level shapefile in QGIS. You can download the data from the following VA public site. Go to the Population Tables and download the “All Veterans Integrated Service Networks” Excel file. It will contain data on the total population at each VISN.

With QGIS, you will need to have two types of files for the data. I recommend using a text editor (not the Windows native notepad) such as Notepad++ or Brackets. In the text editor, open the file with the data and save it as a *.csv. The reason we do this is to make sure that the data is in text format. There are certain values that you want to ensure include the “0” in front of the other numbers (e.g., “01,” “02,” “03,” etc). If you don’t include the “0” you will not be able to join the data to the shapefiles.

View fullsize

After you save this as a *.csv (please include the extension onto the title), then you can open a new document on Notepad++ and enter the data column format. For instance, if column 1 is in text format, then type “String” for the first column. If the second data column is in numeric format, type “Integer.” We have a total of seven columns; therefore, we need to have seven data formats. See the example below.

View fullsize

Step 4: Open QGIS and add the VISN shapefile layer

Click on the Layer tab > Add Layer > Add Vector Layer and browse for the VISN shapefile.

View fullsize

Click on Open and make sure to click Add to add the VISN shapefile onto your QGIS software workspace. You should see the following image appear.

View fullsize

Notice how the polygons are in the form of the VISNs instead of the states. This is an important difference between what you see with the U.S. shapefiles and the VA shapefiles.

Step 5: Add the VISN-level population data

Include the VISN-level population data by downloading it from the VA public site. However, you can also use the Dropbox link that I host with the files already formatted for QGIS here. For this exercise, it would be easier to use the files I provide in the Dropbox link since the formatting may be challenging to implement. For more discussion about the proper formatting, please watch the following video.

You add the VISN-level population data by dragging and dropping it into the Layers panel. Use the file titled “visn_population_2018.csv” and make sure to drop it into the Layers panel. QGIS will automatically recognize the data types because the “visn_population_2018.csvt” file is in the same folder as the “visn_population_2018.csv.”

View fullsize

Step 6: Join the data to the shapefile

Double-click the VISN shapefile in the Layers panel; this will open a new window called the Layers Properties. Click on the JOIN icon and select the data you want to join to the VISN shapefile. Make sure to select VISN for the Join and Target field. This will use the VISN number to join the data to the shapefile. After you select OK, make sure to click on Apply.

View fullsize

Step 7: Adding classes and color

In the Layer Properties window, select the Symbology icon, which will open the menu to add classes and change the color of the different classes. Above the column field, select the Graduated level. In the Column field, select the visn_population_2018_Total, which is the total population of the VISN. Then select Quantile in the Mode field. Change the color ramp field to a blue hue. Click apply and you should immediately see the VISN shapefile file change colors in the workspace.

View fullsize

Your project workspace should look like the following map.

View fullsize

Step 8: Adding labels

Click on the Label icon and select the Single Labels option. Select the Labels variable and then click apply. This may take a while since QGIS has to identify the polygon’s location and insert the labels. The labeling may take about 3-5 minutes because the VISN shapefiles have layers and polygons. I recommend saving this step for when you export the final image generated using the composure function of QGIS to save yourself time.

View fullsize

After the labeling is done, you should see the VISN labels for each polygon.

Step 9: Use the composer to finalize your choropleth

The composer is QGIS’s workspace that allows you to customize the choropleth. Select the composer and name it “VISN population” and then select the sections you want to insert into the composer using the Adds New Map to the Layout icon. Once everything is finalized, you can export this as a *.png or *.pdf file. (At this time, you may turn on the labels if you waited to add these at the very end.)

View fullsize

This is what the choropleth looks like after we finish composing it.

View fullsize

Step 10: Add a coordinate reference system (CRS)

Right now, the map is not an accurate portrayal of the United States in relation to the surface of the Earth. It should be more round at the top due to the distance from the North Pole and the fact that the Earth is a sphere. To ensure that we are accurately portraying the U.S., we need to install the appropriate coordinate reference system (CRS). To do this we need to first click on the Properties of the project and select CRS. We add the CRS from the server using the Datum Transformations window. We change both the Source and Destination CRSs and use the USA_Contiguous_Albers_Equal_Area_Conic CRS (ID = EPSG:102003).

View fullsize

Once the CRS is installed into our CRS database, we can select it to change the shape of the map to correctly conform to the shape of the Earth.

This is what the choropleth looks like in the project workspace.

View fullsize

After we add the labels and compose the final elements, the choropleth looks like the following.

View fullsize

CONCLUSIONS

Using choropleths can highlight important differences across VISNs that would be lost in a table or difficult to present in an alternative chart. Based on the population levels, VISN 22, 17, 10 and 8 have large populations of veterans receiving care at the VA. Areas where there is low prevalence of veterans are in VISN 1, 5, 9, and 15. One thing to consider is that we did not normalize the data based on a single denominator. You can play around with how you want to do that by using the U.S. census, which can be found here. As an added exercise, see if you can create something similar using the U.S. shapefiles, which are located here. Additionally, you can use multiple choropleths (small multiples) to show changes across time or another dimension. Choropleths are excellent visuals that can contribute to a narrative; using the VISN shapefiles will allow you to generate visuals that can enhance a report or presentation.

REFERENCES

I used the following references to develop this tutorial.

https://www.youtube.com/watch?v=aLmMovuydqI&t=387s

https://www.youtube.com/watch?v=rG6UphZGmg4&t=615s

https://www.youtube.com/watch?v=LNJj3g6SRqU

Download QGIS here:

https://www.qgis.org/en/site/forusers/download

VA population data:

https://www.va.gov/vetdata/veteran_population.asp

VISN shapefiles:

https://catalog.data.gov/dataset/veterans-integrated-services-networks-visn-markets-submarkets-sectors-and-counties-by-geog

Using inverse probability of treatment weights & Marginal structural models to handle time-varying covariates

BACKGROUND

When constructing regression models, there are two approaches to handling confounders: (1) conditional and (2) marginal approaches.(1) The conditional approach handles confounders using stratification or modeling (e.g., adding covariates to be regressed to the outcome). Whereas, the marginal approach uses weights to balance the confounders across treatment exposure levels.(1–5) In conventional regression models, the exposure is regressed to the outcome controlling for potential confounders. However, in longitudinal data, time-varying confounders can result in biased estimates of the model parameters if not properly adjusted. This gets more complicated when we have a time-varying exposure in the model to account for.

In panel data analysis or longitudinal data analysis, adjusting for time-varying exposure and time-varying confounders are critical to reducing bias. Additionally, there are time-dependent relationships between the confounders and exposure that need to be considered when adjusting for longitudinal regression models. In this article, we will focus on the marginal approach in terms of using the inverse probability of treatment weights fitted to a marginal structural model.

This article was published on RPubs with the corresponding R code using RMarkdown and can be located at this link.

 

TIME-DEPENDENT RELATIONSHIPS

In Figure 1, the time-dependent relationships between times 1 and 0 for the treatment variable are indicated by the arrows (We look at the relationships across two time points. In actual longitudinal data, there may be more than two time points to consider). Notice how the Outcome at time==0 is a confounder for the relationship between Exposure and Outcome at time==1.

Figure 1. Time-dependent relationships between the exposure and outcome variables.

Conventional methods to perform longitudinal data analysis such as linear mixed effects models and generalized estimating equations models are capable of handling time-varying covariates. However, in the case of a time-varying elements, the probability of treatment exposure is invariably different across time, which requires application of time-varying weights on the unit of analysis (e.g., individual subjects).

We can address this issue by applying inverse probability of treatment weights (IPTW) to the observations, which are then fitted to a marginal structural model (MSM).(4,5) IPTW are used to make the exposure at time 0 and 1 independent of the confounders that occur beforehand and allow us to generate a causal interpretation between the treatment exposure on the outcome.

DESCRIPTION OF METHODS

IPTW are weights assigned to each observation across time conditioned on the previous exposure history, which are then multiplied to generate a single weight for a subject. Similar to conventional propensity score estimation, IPTW is generated using either a logit or probit model that regresses covariates to a treatment group (exposure) variable. With IPTW, the previous exposure history is incorporated to the propensity score estimation, which is time-varying.

Standardized weights in a longitudinal setting are estimated as

where A is the exposure for subject i at time t_ij (time points range starting at k = 0 to k=j). The numerator contains the probability of the observed exposure at each time point (a_ik) conditioned on the observed exposure history of the previous time point (a_ik-1) and the observed non-time varying covariates (v_i). The denominator contains the probability of the observed exposure at each time point conditioned on the observed exposure history of the previous time point (a_ik-1), the observed time-varying covariates history at the current time point (c_ik), and the non-time varying covariates (v_i).

In standardized weights, the time-varying confounders are captured in the denominator but not in the numerator. However, the non-time varying (also known as fixed-time) covariates are captured in both the numerator and denominator to stabilize the weights. Using stabilized weights is preferable to non-standardized weights, which are not discussed in this article.

Some statistical software are unable to handle time-varying weights; hence, a single weight for each individual needs to be estimated. Once the standardized weights for subject i at time t_ij are calculated, a single weight is estimated by multiplying all the standardized weights across the time points, which is then applied in a marginal structural model for subject i.

There are several key assumptions that must be made in order for IPTW methods to generate causal interpretation between the exposure and outcome (Thoemmes and colleagues provides a detailed explanation in their paper)(5):

1) No unmeasured confounding

2) Positivity

3) Correct specification of the IPTW

Given these assumptions are met, using IPTW fitted to an MSM can yield causal inference between the treatment exposure and outcome. This method is flexible enough where it can be applied to a linear mixed effects model, generalized estimating equation model, and survival model. Gerhard and colleagues used this approach (marginal structural Cox model) to estimate the treatment effects of antihypertensive therapy in a non-randomized trial.(6) Hernan and colleagues used a marginal structural Cox proportional hazard model to estimate the treatment effect of zidovudine and Pnuemocystis carinii therapy on survival of HIV-positive homosexual males in a non-randomized trial.(4)  

MOTIVATING EXAMPLE

This article will use CRAN R program statistical software to perform the IPTW fitted to an MSM. We will use the data that was simulated using the following R commands.

#set seed to replicate results
set.seed(12345)

#define sample size
n <- 2000

#define confounder c1 (gender, male==1)
male <- rbinom(n,1,0.55)

#define confounder c2 (age)
age <- exp(rnorm(n, 3, 0.5))

#define treatment at time 1
t_1 <- rbinom(n,1,0.20)

#define treatment at time 2
t_2 <- rbinom(n,1,0.20)

#define treatment at time 3
t_3 <- rbinom(n,1,0.20)

#define depression at time 1 (prevalence = number per 100000 population)
d_1 <- exp(rnorm(n, 0.001, 0.5))

#define depression at time 2 (prevalence = number per 100000 population)
d_2 <- exp(rnorm(n, 0.002, 0.5))

#define depression at time 3 (prevalence = number per 100000 population)
d_3 <- exp(rnorm(n, 0.004, 0.5))

#define tme-varying confounder v1 as a function of t1 and d1
v_1 <- (0.4*t_1 + 0.80*d_1 + rnorm(n, 0, sqrt(0.99))) + 5

#define tme-varying confounder v2 as a function of t1 and d1
v_2 <- (0.4*t_2 + 0.80*d_2 + rnorm(n, 0, sqrt(0.55))) + 5

#define tme-varying confounder v3 as a function of t1 and d1
v_3 <- (0.4*t_3 + 0.80*d_3 + rnorm(n, 0, sqrt(0.33))) + 5

#put all in a dataframe and write data to harddrive to use later in e.g. SPSS
df1 <- data.frame(male, age, v_1, v_2, v_3, t_1, t_2, t_3, d_1, d_2, d_3)

write.table(round(df1,11),"data1.csv", row.names = FALSE, quote = FALSE)

A little data manipulation was done to make treatment in the following period equal to 1 if the previous period was also equal to 1. In other words, E[Treatment=1, time=1 | Treatment=1, time=time-1]. Age was rounded to the nearest whole number. You can download the *CSV file here.

The dataset contains variables for id, male, age, treatment (t), outcome (d), time-varying covariate (v), and time. Exploring the dataset set, we see the structure as:

There are 2000 individuals with three repeated measures of the t, v, and d variables. The t variable represents the Treatment exposure, which is time-varying. The v variable represents an arbitrary time-varying covariate. And the d variable is the outcome (dependent) variable, which is also time-varying. Non-time varying covariates include the age at baseline and the gender of each individual.

LONGITUDINAL DATA ANALYSIS APPROACH

Generalized estimating equations (GEE) were constructed to evaluate the impact of the treatment (t) on the outcome (d) and to handle the time-varying covariate (v) in the panel dataset. Since the outcome was a continuous variable, a generalized linear Gaussian family with identity link was used. Auto-regressive (AR1) correlation structure was selected since this was a time series (panel) data; we expected the correlation to decay as the outcome values were farther away from the time of interest. 

We will need the following packages:

geepack

survey

ipw

reshape

deplyr

The following R code was used to generate the IPTW and fitted to a MSM using GEE.

#######################################################################
# Install the required packages
#######################################################################
library(geepack)
library(survey)
library(ipw)
#library(foreign)
#library(multcomp)
#library(gee)
library(reshape)
library(dplyr)

#######################################################################
#Estimate ipw weights (time-varying)
#######################################################################
# estimate inverse probability weights (time-varying) using a logistic regression
w <- ipwtm(
  exposure = t,
  family = "binomial",
  link = "logit",
  numerator = ~ factor(male) + age,
  denominator = ~ v + factor(male) + age,
  id = id,
  timevar=time,
  type="first",
  data = data_long_sort)
summary(w$ipw.weights)

iptw = w$ipw.weights


# Add the iptw variable onto a new dataframe = data2.
data2 <- cbind(data_long_sort, iptw)

#######################################################################
# Plot the stabilized inverse probability weights
#######################################################################
ipwplot(weights = data2$iptw, 
        timevar = data2$time, 
        binwidth = 0.5,
        main = "Stabilized weights", 
        xaxt = "n",
        yaxt = "n")

#######################################################################
# confint.geeglm function (to generate 95% CI for the geeglm())
#######################################################################
confint.geeglm <- function(object, parm, level = 0.95, ...) {
  cc <- coef(summary(object))
  mult <- qnorm((1+level)/2)
  citab <- with(as.data.frame(cc),
                cbind(lwr=Estimate-mult*Std.err,
                      upr=Estimate+mult*Std.err))
  rownames(citab) <- rownames(cc)
  citab[parm,]
}


#######################################################################
# GEE model #1.1 - GEE with cluster robust SE (no IPTW)
#######################################################################
gee.bias <- geeglm(d~t + time + factor(male) + age + cluster(id),
                    id=id,
                    data=data2, 
                    family=gaussian("identity"), 
                    corstr="ar1")
summary(gee.bias)
confint.geeglm(gee.bias, level=0.95)

#######################################################################
# GEE model #2 - IPTW fitted to MSM with clustered robust SE
#######################################################################
gee.iptw <- geeglm(d~t + time + factor(male) + age + cluster(id),
                   id=id,
                   data=data2, 
                   family=gaussian("identity"), 
                   corstr="ar1", 
                   weights=iptw)
summary(gee.iptw)
confint.geeglm(gee.iptw, level=0.95)

We compared the findings from the convention GEE model without IPTW to the GEE model incorporating IPTW (Table). The differences are significant. In the standard GEE model, the treatment (t) is associated with a reduction in the outcome (d) by 0.012 units with a 95% confidence interval (CI) of -0.020 and 0.045, which is not statistically significant. Conversely, in the GEE model incorporating IPTW, the treatment (t) is associated with a reduction in the outcome (d) by 0.071 units with a 95% CI of -0.104 and -0.038, which is statistically significant. 

 

CONCLUSIONS

Based on our findings, the IPTW fitted to a MSM (GEE model) resulted in a statistically significant reduction in the treatment on the outcome that would not have otherwise been captured in the conventional GEE model. Given that there are time-varying covariates (especially with the treatment variable), IPTW fitted to a MSM may yield important differences that would otherwise be unidentified with conventional methods. However, it is critical that all assumptions regarding the IPTW method are satisfied prior to accepting the model’s results.

 

REFERENCES

1. Williamson T, Ravani P. Marginal structural models in clinical research: when and how to use them? Nephrol Dial Transplant. 2017 Apr 1;32(suppl_2):ii84–90.

2. Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiol Camb Mass. 2000 Sep;11(5):550–60.

3. Hernán MA, Hernández-Díaz S, Robins JM. A structural approach to selection bias. Epidemiol Camb Mass. 2004 Sep;15(5):615–25.

4. Hernán MA, Brumback B, Robins JM. Marginal Structural Models to Estimate the Joint Causal Effect of Nonrandomized Treatments. J Am Stat Assoc. 2001 Jun 1;96(454):440–8.

5. Thoemmes F, Ong AD. A Primer on Inverse Probability of Treatment Weighting and Marginal Structural Models. Emerg Adulthood. 2016 Feb 1;4(1):40–59.

6. Gerhard T, Delaney JA, Cooper-DeHoff RM, Shuster J, Brumback BA, Johnson JA, et al. Comparing marginal structural models to standard methods for estimating treatment effects of antihypertensive combination therapy. BMC Med Res Methodol. 2012 Aug 6;12:119.

Communicating data effectively with data visualizations - Part 10 (Heat Maps)

BACKGROUND

A heat map is a data visualization tool that uses positioning and coloring to identify clusters and correlations in multivariable analysis. The most common type of heat map is a 2 x 2 matrix, where two variables are examined using the rows and columns (R x C) positions on a matrix. A heat map matrix helps us identify any patterns or similarities across the different dimensions. In a heat map, color is critical in denoting degrees of change. (Please see refer to the past blog on colors.)

For example, we can see the changes in opioid overdose rates across time for each state (Figure 1). As the rates increase, the cells are darker (indicated by the legend). All the states experience an increase in opioid overdose deaths, but State 1 is experiencing it faster than States 2 and 3.

In this tutorial, we will perform two methods to create heat maps. The first method will use the built in Excel conditional formatting rules and the second method will use VBA macros.

Figure 1. Heat map matrix.

MOTIVATING EXAMPLE

We will continue to use the state-level drug overdose mortality data from the CDC.

https://www.cdc.gov/drugoverdose/data/statedeaths.html

Mortality rate is presented as the number of deaths per 100,000 population.

In this tutorial, we will develop a heat map using opioid overdose mortality from 2013 to 2016.

The data setup in Excel has State indicators as the rows and time indicators as the columns. We are visualizing the change in opioid overdose mortality from 2013 to 2016 for each state. Figure 2 illustrates the data structure for the first seven states.

Figure 2. Data structure for the first seven states.  

METHOD 1: CONDITIONAL FORMATTING RULES

Excel has a convenient tool that allow us to use conditional formatting to shade our heat map matrix.

Step 1: First highlight all the data.

Step 2: In the Excel Ribbon, select Conditional formatting and then New.

Step 3: Select “Format all cells based on their values” and change the Format Style to “3-Color scale.” Change the color to the different shades you are interested in using. (In this example, we used a blue base with varying degrees of shading.) Select percentile and then click “Ok.” The percentile will use the Median for each column to distinguish the middle category for the rates of opioid overdose mortality for each state.

Step 4: Visually inspect the results. If there are no apparent pattern in the heat map, we will need to sort the rate of opioid overdose mortality for 2016 in descending order.

The heat map should look like the following:

There is a pattern emerging in regards to the rate of opioid overdose mortality across the different states. West Virginia has the highest opioid overdose mortality rate in 2016, but they also appear to have the highest from 2013 to 2015. The dark cell in 2016 indicates that West Virginia has exceeded the 50 deaths per 1000 population incidence rate. Other states also have high rates of opioid overdose mortality across 2013 to 2016, which continued to increase. The 2013 column is clearly lighter indicating that the opioid overdose mortality has increased over time up to the available data in 2016.

Step 5: We can improve this heat map by removing the numbers, which can be distracting. We need to select all the data and format the cells. Select only the numeric data and then format the number. Use the “Custom” category and enter the following: "";"";"";"". This will change the number values so that it doesn’t show in the cells.

Step 6: Change the column width and row height so that you have a nice square-like matrix for the final result. We used a column width of 5 and a row height of 30. (Only the first fifteen states are shown.)

View fullsize

The heat map can be used to quickly identify states with the highest opioid overdose mortality and the trends across time. The states with the highest rates of opioid overdose mortality are clustered at the top while the states with the lowest rates are clustered at the bottom.

We could also arrange this into regions of the US to further stratify the results (not shown).

METHOD 2: USING VBA MACROS FOR CONDITIONAL FORMATTING OF MORE THAN 3 CATEGORIES

Excel only allows us to choose up to 3-Color scales. If we wanted to use more than 3 color categories, we will need to use VBA macros.

But before we do, we need to think about the colors for the scales. Since we have more than 3 categories, we will need to figure out how to divide the colors.

COLOR CODES

We will need to determine the base color for our heat map. In this example, we will use a blue base-color and change the shading using the RGB color values. RGB colors are based on a system using a combination of three base colors (red, green, and blue) that can be used to change the intensity of the color from a range between 0 and 250. An example of an RGC color table can be found in the following site.

For this example, we used the following RGB color values where dark-navy denotes high rates of opioid overdose mortality (50 or more per 1000 population). However, you can change the values of these colors however you like.

We will continue to use the blue color base and change the gradient using the RGB values.

VISUAL BASIC FOR APPLICATION (VBA) MACRO

The VBA macro comes from the site Excel For Beginners and written by Kristoff deCunha. We used the VBA code on the site, but modified it for this tutorial.

The VBA code is written in a way where any changes in the values will automatically update the color of the cell. Additionally, the code also sorts the 2016 opioid overdose mortality rate in descending order, adds thin-white continuous borders around the cells, and changes the font to Times New Roman.

Here are the VBA macros used for Method 2.

Macro 1 changes the font to Times New Roman.

‘Macro1
Sub ChangeFont()

Dim rng As Range
Set rng = Range("J1:N52")

With rng.Font
    .Name = "Times New Roman"
    .Size = 12
    .Strikethrough = False
    .Superscript = False
    .Subscript = False
    .OutlineFont = False
    .Shadow = False
    .Underline = xlUnderlineStyleNone
    .ThemeColor = xlThemeColorLight1
    .TintAndShade = 0
    .ThemeFont = xlThemeFontNone
End With

End Sub

Macro 2 changes the cell shading to the 6-Color scale (blue-base)

‘Macro2
Sub ChangeCellColor()


Dim rng As Range
Dim oCell As Range

Set rng = Range("K2:N52")

For Each oCell In rng
        Select Case oCell.Value
                 Case 50 To 100
                     oCell.Interior.Color = RGB(37, 54, 97)
                     oCell.Font.Bold = True
                     oCell.Font.Name = "Times New Roman"
                     oCell.HorizontalAlignment = xlCenter
                 Case 40 To 49.999
                     oCell.Interior.Color = RGB(56, 83, 145)
                     oCell.Font.Bold = True
                     oCell.Font.Name = "Times New Roman"
                     oCell.HorizontalAlignment = xlCenter
                 Case 30 To 39.999
                     oCell.Interior.Color = RGB(147, 168, 215)
                     oCell.Font.Bold = True
                     oCell.Font.Name = "Times New Roman"
                     oCell.HorizontalAlignment = xlCenter
                 Case 20 To 29.999
                     oCell.Interior.Color = RGB(183, 198, 228)
                     oCell.Font.Bold = True
                     oCell.Font.Name = "Times New Roman"
                     oCell.HorizontalAlignment = xlCenter
                 Case 10 To 19.999
                     oCell.Interior.Color = RGB(218, 225, 240)
                     oCell.Font.Bold = True
                     oCell.Font.Name = "Times New Roman"
                     oCell.HorizontalAlignment = xlCenter
                 Case 0 To 9.999
                     oCell.Interior.Color = RGB(230, 237, 253)
                     oCell.Font.Bold = True
                     oCell.Font.Name = "Times New Roman"
                     oCell.HorizontalAlignment = xlCenter
                  Case Else
                     oCell.Interior.ColorIndex = xlNone
         End Select
    Next oCell
    
End Sub

Macro 3 sorts the 2016 opioid overdose mortality rates in descending order.

‘Macro3
Sub SortColumn()

Dim DataRange As Range
Dim keyRange As Range
Set DataRange = Range("J1:N52")
Set keyRange = Range("N1")
DataRange.Sort Key1:=keyRange, Order1:=xlDescending

End Sub

Macro 4 hides the font from the heat map.

‘Macro4
Sub HideFont()
    
Dim rng As Range
Dim oCell As Range

Set rng = Range("K2:N52")

    For Each oCell In rng
        oCell.Font.Color = oCell.Interior.Color
    Next oCell
    
End Sub

Macro 5 creates thick white borders for each cell in the table.

‘Macro5
Sub WhiteOutlineCells()

    Dim rng As Range

    Set rng = Range("J1:N52")

    With rng.Borders
        .LineStyle = xlContinuous
        .Color = vbWhite
        .Weight = xlThick
    End With
    
End Sub

INSERTING DATA AND RUNNING MACRO

The five macros are assigned to a button in the Excel Macro-Enabled Workbook. Pressing the button will perform the task of creating a 6-Color scale heat map. Download the Excel Macro-Enabled Workbook here. This file will have the raw data and the macro-enabled worksheet for you to create a heat map.

Step 1: Copy the raw data from the “combined” worksheet.

Step 2: Paste it in the worksheet “heatmap_2” starting on cell "J1".

Step 3: Then press the “PressStart” button to run the macros. Your final heat map should look like the following:

View fullsize

Compare the heat map from Method 1 (3-Color scale) to the one generated by Method 2 (6-Color scale). The heat map with the 6-Color scale has a lighter pattern compared to the 3-Color scale heat map. The differences are dramatic. Depending on the granularity of the heat map you want, either one of these color scales would be fine. However, Method 2 requires some VBA coding.

View fullsize

* Not all states shown.

Conclusions

Heat maps allow us to observe patterns in the data. In our example, we notice that West Virginia has a high rate of opioid overdose mortality indicated by the clustering of dark cells from 2013 to 2016. Other states had similar patterns as West Virginia. Using heat maps provides a quick and easy interpretation of the changes in opioid overdose mortality across time and the states that are clustered together that have high rates of opioid overdose mortality.

REFERENCES

I used the following websites to help develop this tutorial.

Conditional formatting with more than 3 categories:
https://sites.google.com/site/excelforbeginners/Home/vba-codes/conditional-formatting-more-than-3-criterias
 
Changing the RGB color codes:
https://analysistabs.com/excel-vba/change-background-color-of-cell-range/
https://www.w3schools.com/colors/colors_rgb.asp

Excel color palette library:
http://dmcritchie.mvps.org/excel/colors.htm

Excellent site for VBA coding:
https://www.excel-easy.com/vba.html

Communicating data effectively with data visualizations - Part 9 (Cleveland Plots)

BACKGROUND

Visualizing change across two time points allows your audience to see the impact of a program’s impact. In a previous article, I demonstrated how you can use slope graphs to illustrate changes across two time points. However, there is a risk of the slope graphs becoming a tangled mess (or spaghetti plot) if too many comparisons are being made. An easier way to illustrated changes cross two time points for a large number of groups is with a Cleveland dot plot (or lollipop plot).

By using a horizontal line between two points arranged from most change to least change, your audience can quickly visualize the program’s impact and rank them according to the subject or group.

MOTIVATING EXAMPLE

We will continue to use the state-level drug overdose mortality data from the CDC.

https://www.cdc.gov/drugoverdose/data/statedeaths.html

Mortality rate is presented as the number of deaths per 100,000 population.

In a previous tutorial, we only looked at eight different states. In this tutorial, we will illustrate a change in all 50 states onto a single plot using a Cleveland plot.

Here is the data setup in Excel:

The difference is calculated as the difference in mortality rates between 2016 and 2010.

In Excel, select the first two rows (State and 2016 rate) and generate a horizontal bar chart. Make sure to sort the order of the 2016 rate from least to greatest.

The horizontal bar chart should look like the following:

After you created the horizontal bar plot, you will need to add error bars. Select the Design tab > Add Chart Elements > Error Bars > More Error Bars Options:

In the Format Error Bars options, make sure to check Minus under Directions, No Cap under End Style, and Custom under Error Amount:

Click Specify Value and then select the differences column for the Negative Error Value:

On the bar chart, select the bars and then under the Format

The horizontal bar chart should have the fill remove and the error bars present and should look like the following:

Select the error bar and go to the Format Error Bars option. Under the Joint type select Round and under the Begin Arrow Size select the Oval Arrow. This will add a circle on the one end of the error bar.

You can also increase the size of the Oval Arrow by selecting a larger size from the Begin Arrow Size drop down.

After selecting the Oval Arrow for the Join Type and the Begin Arrow Type, your chart should look like the following:

The next steps will require you to add a second data series. Right-click on the chart area and select the 2010 mortality rates.

After selecting the data, make sure to map the Horizontal Axis Labels to the corresponding states.

Your chart should now include the second data series (2010 mortality rates) as horizontal bars.

In the next steps, you will add error bars to the 2010 mortality horizontal bars (similar to the error bars for the 2010 mortality rates data). Instead of adding error bars for the Minus, you will add error bars for the Plus.

Similar to the 2016 mortality rates data, you will remove the horizontal bars by selecting No fill and then setting the Series Overlap to 100%

Select the error bars and then change the Begin Arrow Type to Oval and increase the size.

Your chart should now include two dots with lines between them for each state.

After a few more adjustments to the dot size and colors, the final Cleveland plot can look like the following:

Figure 1. Cleveland plot comparing the drug overdose mortality rates between 2010 and 2016.

The dots give us a good illustration of the magnitude of change in the drug overdose mortality rates between 2010 and 2016. Additionally, using the colored fonts help to map the drug overdose mortality values with the dots. For example, West Virginia had the highest drug overdose mortality rate in 2016 (blue dot) and a large increase in drug overdose mortality rates between 2010 (red dot) to 2016. Nebraska has the lowest drug overdose mortality rate in 2016 (blue dot) among the states, which was lower than in 2010 (red dot).

CONCLUSIONS

Cleveland plots can illustrate the change in drug overdose mortality rates between two time points for multiple groups without cluttering the chart space. Unlike slope graphs which can be difficult to distinguish between states, the Cleveland plot separates each state into their own rows allowing for a simple estimation of change across two time points. Moreover, it is also easier to see the magnitude in change in between 2010 and 2016. We recommend using Cleveland plots when you have a lot of groups (e.g., states) with an outcome that changes across two time points (2010 and 2016).

REFERENCES

I used the following websites to help develop this tutorial.

http://stephanieevergreen.com/lollipop/

https://policyviz.com/2016/02/04/lollipop_graph_in_excel/

https://zebrabi.com/lollipop-charts-excel/

https://peltiertech.com/dot-plots-microsoft-excel/

The following video provides step-by-step instructions in making a horizontal lollipop chart:

https://www.youtube.com/watch?v=tHa8eEb-LTg

The following website provides examples of lollipop charts:

https://www.r-graph-gallery.com/lollipop-plot/

Communicating data effectively with data visualizations - Part 8 (Slope graphs)

BACKGROUND

Suppose you wanted to show a change across two periods in time for several groups. How would you do that? One of the best data visualizations for this is the slope graph. In this tutorial, we’ll show you how to create a slope graph in Excel and highlight a state using contrasting colors.

MOTIVATING EXAMPLE

We will use the state-level drug overdose mortality data from the CDC.

https://www.cdc.gov/drugoverdose/data/statedeaths.html

Here is a sample of set of data from the CDC:

Each value is a rate for the number of deaths per 100,000 population.

In Excel, select the three columns (State, 2010 rate, and 2016 rate).

Go to Insert Chart and select Line with Markers.

The chart should look like the following:

Right-click anywhere on the chart and click Select Date and then click on the Switch Row/Column.

The Y and X axes should switch places and the chart should look like the following:

Delete the Chart title, legend, and Y-axis.

Right-click on the X-axis and select Format Axis. Then select “On tick marks.”

This will move the lines to the edges of the chart.

Now, we want to add labels to the ends of each line. Right click on one of the lines and select Add Data Labels. Then select the left data label and format it according to the following guide:

Do the same thing for the right label, but make sure to use the right label position. Bring both ends of the chart closer to the middle to give your data labels room to expand (otherwise, the state will stack on top of the value, which you do not want). The chart should look like the following:

Finally, you can format the figure using different colors and removing the excess gridlines. Try to experiment with different shades of color to generate the desired effect. In our example, we wanted to highlight West Virginia from the rest of the other states.

Here is what the slope graph looks like after some tweaking and adjustments:

In the above slope graph, West Virginia was highlighted using a cranberry color to give it a greater contrast to the lighter grey of the other states. You could use this method to highlight other states of interest such as New Hampshire or the District of Columbia, which had greater percentage increases between 2010 and 2016.

In the final slope graph, we highlight West Virginia and New Hampshire in different colors to distinguish them from the other states.

CONCLUSIONS

Using slope graphs can show simple trends across two periods in time. More complex slope graphs can have multiple time points and more states. In our simple example, we highlight the key steps to generate a slope graph in Excel. Using colors to highlight certain states can make a simple slope graph more visually appealing and assist the eyes in identifying the states that are important according to the data.

REFERENCES

Knaflic, CN. Storytelling with Data. 2015. John Wiley & Sons, Inc., Hoboken, New Jersey.

Estimating marginal effects using Stata Part 1 – Linear models

BACKGROUND

Regression models provide unique opportunities to examine the impact of certain predictors on a specific outcome. These predictors’ effects are usually isolated using the model coefficients adjusting for all other predictors or covariates. A simple linear regression model with a single predictor x_i is represented as

where y_i denotes the outcome (dependent) variable for subject i, beta0 denotes the intercept, beta1 is the model coefficient that denotes the change in y due to a 1-unit change in x, and epsilon_i is the error term for subject i.

A 1-unit increase in x is associated with some change in the outcome y. This finding may explain predictor variable x’s impact on outcome variable y, but it doesn’t not tell us the impact of a representative or prototypical case.

The marginal effect allows us to examine the impact of variable x on outcome y for representative or prototypical cases. For example, Stata’s margins command can tell us the marginal effect of body mass index (BMI) between a 50-year old versus a 25-year old subject.

There are three types of marginal effects of interest:

1.       Marginal effect at the means (MEM)

2.       Average marginal effect (AME)

3.       Marginal effect at representative values (MER)

Each of these marginal effects have unique interpretations that will impact how you examine the regression results. (We will focus on the first two, since the third one is an extension of the AME.) The objective of this tutorial is to review these marginal effects and understand their interpretations through examples using Stata.

 

MOTIVATING EXAMPLE

We will use the Second National Health and Nutrition Examination Survey (NHANES) data from the 1980s, which can be found in Stata’s library using the following command:

use http://www.stata-press.com/data/r15/nhanes2.dta

Table 1 summarizes the characteristics of the NHANES population.

 

ADJUSTED PREDICTIONS

Adjusted prediction for a regression model provides the expected value of an outcome y conditioned on x assuming all other things are equal. In other words, this is the effect of the predictor variable x regressed to outcome variable y adjusting or controlling for other covariates. Therefore, if you were comparing the effect of a 1-unit increase in age to the BMI, then you could compare this across all patients who are equally White, Black, or Others.

Example 1

A simple linear regression model can capture the incremental effect of age on body mass index. For example, the impact of age on body mass index (BMI) can be represented as a linear regression:

where BMI_1  is the body mass index for individual i, beta0 denotes the intercept (or BMI when AGE=0), beta1 denotes the change in BMI for each 1-unit increase in Age for individual i, and episilon_i denotes the error term for individual i. (The unit of BMI is kg/m^2).

The Stata command to perform a simple linear regression:

regress bmi age

The corresponding regression output is:

In this regression output example, the predictor of interest is AGE. The _cons parameter denotes the coefficient beta0 otherwise known as the intercept; therefore, a subject with AGE = 0 has a BMI that is 23.2 kg/m^2. (Although this is unrealistic, we will ignore this for now.) The impact AGE has on the BMI is denoted by the slope parameter beta1, which is the change in BMI due to a 1-unit change in Age. In this example, the a 1-unit increase in Age is associated with a 0.05 kg/m^2 increase in BMI.

If we wanted to know the difference in BMI between a 50-year old and 25-year old, we need to estimate the adjusted prediction, which estimates the difference in the outcome based on some user-defined values for the x variables.

To estimate the adjusted predicted BMI for a 50-year old, we used the following equation:

which is 25.7 kg/m^2. We can do this using the following Stata command:

di _b[_cons] + 50*_b[age]
25.655896

Similarly, we can estimate the adjusted predicted BMI for a 25-year old:

which is 24.4 kg/m^2.

The difference between these two is:

25.655896 - 24.433991 = 1.2 kg/m^2. 

Therefore, the difference in BMI between a 50-year old and 25-year old is on average 1.2 kg/m^2. This seems like a tedious process, but let’s see how we can make this exercise simpler using Stata’s margins command.

We can use Stata’s margins command to estimate the adjusted predicted BMI for a 50-year old and 25-year old:

margins, at(age=(25 50))

Figure 2. Stata’s margins command output for adjusted prediction of BMI for a 50-year old and 25-year old.

Example 2

We use a linear regression with other independent variables to illustrate the complexity of having other covariates adjusted in the model.

The regression model has the structure:

where  is the body mass index for individual i, beta0 is the intercept (or BMI when AGE=0), beta1 is the change in BMI for each 1-unit increase in Age for individual i, beta2 denotes the change in BMI for a female relative to a male, beta3 denotes the change in BMI due to contrasts in race categories (White, Black, and Other), and  is the error term for individual i. (The unit of BMI is kg/m^2).

For this example, RACE will be included into the regression model as a dummy variable using the following Stata command:

regress bmi age i.race i.sex

The corresponding regression output is:

The following are interpretations of the regression output.

A 1-unit increase in age is associated with a BMI increase of 0.05 kg/m^2 adjusting for race and sex or all things being equal.

Blacks are associated with a BMI increase of 1.4 kg/m^2 adjusting for age and sex compared to Whites.

Others are associated with a BMI decrease of 1.2 kg/m^2 adjusting for age and sex compared to Whites.

Females are associated with a BMI increase of 0.03 kg/m^2 adjusting for age and race.

If we wanted to know the adjusted prediction for a 50-year old and 25-year old, we can use the margins command:

margins, at(age=(25 50)) atmeans vsquish

The output is similar to Example 1 but there are some differences.

The atmeans option captures the “average” sample covariates. In our example, the mean proportion of females is 0.525, males is 0.475, Whites is 0.876, Blacks is 0.105, and Others is 0.019. Therefore, the adjusted predictions for 50-year old and 25-year old’s BMI is conditioned on the “average” values of the covariates in the model. This may not make sense because an individual subject can’t be 0.525 female and 0.475 male. Fortunately, we have other ways to address this with the marginal effect.

 

MARGINAL EFFECT

Marginal effect with the margins command generates the change in the conditional mean of outcome y with respect to a single predictor variable x. In other words, this is the partial effect of x on the outcome y for some representative or prototypical case. Usually this is obtained by performing a first-order derivative of the regression expression:

where the partial effect of the expected value of y condition on x is the first order derivative of the expected value of y condition on x with respect to x.

The representative or prototypical case can be the mean, observed, or a user defined case.

MARGINAL EFFECT OF THE MEAN (MEM)

MEM is the partial effect of on the dependent variable (y) conditioned on a regressor (x) after setting all the other covariates (w) at their means. In other words, MEM is the difference in x’s effect on y when all other covariates (RACE and FEMALE) are at their mean.

Let’s revisit the linear regression model but with the dummy variables included:

In the output the beta1 = 0.0493881.

Getting the partial effect with respect to Age at the means for the other covariates, we use the following command:

regress bmi age i.race i.sex

margins, dydx(age) atmeans vsquish

Interpretation: For a subject who is average on all characteristics, the marginal change of a 1-unit increase in age is a 0.049 increase in the BMI.

We can also look at the MEM at different ages (e.g., 25 and 50 years):

margins, dydx(age) at(age=(25 50)) atmeans vsquish

This command performs the MEM for 25- and 50-year old subjects with their covariates set at the population mean. We interpret the results as the effect of age at different values of age at the average values of the other covariates.

The MEM should be:

The effect of age at 25 and 50 years old is an increase of 0.05 years. Notice that the MEM for 25- and 50-year olds are the same (MEM = 0.0493881). This is because the model is a linear regression. For every incremental increase in age, the incremental increase in the BMI is 0.0493881 given the other covariates are set at the mean.

To illustrate, we can manually perform this operation using the information above. Recall that the linear regression model with the dummy variables is represented as:

BMI for a 25-year old subject at the mean = intercept + 25*(beta1) + (mean of Black)*(beta2) + (mean of Other)*(beta3) + (mean of Female)*(beta4) = 24.42243 kg/m^2.

BMI for a 25-year old subject at the mean = 23.0528 + 25*(0.0493881) + .1049174*(1.382849) + .0193218*(-1.2243) + .5251667*(.025702) = 24.42243 kg/m^2, which is the same as the value presented in the adjusted prediction output.

Why are these the same? The linear regression is predictable in terms of the slope coefficients. Therefore, an incremental increase in predictor variable x will have the same incremental marginal increase in outcome variable y. When you apply the MEM to non-linear models, the slopes are no longer linear and will change based on varying levels of the continuous predictor x.

AVERAGE MARGINAL EFFECT (AME)

Unlike the MEM the average marginal effect (AME) doesn’t use the mean for the covariates when estimating the partial effect of the predictor variable x on the outcome variable y. Rather, the AME estimates the partial effect of the variable x on the outcome variable y for using the observed values for the covariates and then the average of that partial effect is estimated. In other words, the partial derivative is estimated with respect to x using the observed values for the other covariates (RACE and FEMALE), and then the average of that first-order derivative are averaged over the entire population to yield the AME. This is represented as:

where the partial derivative of the estimated value of the outcome variable y with respect to x is conditioned on the values of covariates (w) for subject i over the entire population (N) and multiplied by beta_k (or the parameters of interest) .

Getting the partial effect with respect to Age at the observed values for the other covariates, we use the following command:

regress bmi age i.race i.sex

margins, dydx(age) asobserved vsquish

Interpretation: The average marginal effect of a 1-unit increase in age is a 0.049 increase in the BMI.

We can also look at the AME at different ages (e.g., 25 and 50 years):

margins, dydx(age) at(age=(25 50)) asobserved vsquish

This command performs the MEM for 25- and 50-year old subjects with their covariates set at the observed values. We interpret the results as the effect of age at different values of age at the observed values of the other covariates.

The AME should be:

The effect of age at 25 and 50 years old is an increase of 0.05 years. Notice that the AME for 25- and 50-year olds are the same (MEM = 0.0493881). Similar to the MEM, this is because the model is a linear regression. For every incremental increase in age, the incremental increase in the BMI is 0.0493881 given the other covariates are set at the observed values.

CONCLUSIONS

We see that the MEM and AME are exactly the same because of the linear model. The marginal effect of an increase in 1-unit of age is an increase in 0.05 kg/m^2 of the BMI. In the next part, non-linear models will be used to demonstrate that the MEM and AME are not equal.

REFERENCES

I used the following websites to help create this tutorial:

https://thomasleeper.com/margins/articles/Introduction.html

https://support.sas.com/rnd/app/ets/examples/margeff/index.html

https://www.ssc.wisc.edu/sscc/pubs/stata_margins.htm

I also used the following paper by Richard Williams:

Using the margins command to estimate and interpret adjusted predictions and marginal effects. The Stata Journal. 2012;12(2):308-331.

https://www.stata-journal.com/article.html?article=st0260

CHOICE Blog: Trump Administration’s Blueprint to Address Drug Prices

I wrote a piece about the Trump Administration's plans to address drug prices, which was published on The CHOICE Institute Blog, Incremental Thoughts, on 16 May 2018. I summarized the key points from the Trump Administration and highlighted an interview by The CHOICE Institute alumnus, Dr. Jonathan H. Watanabe, Associated Professor of Clinical Pharmacy at the UCSD Skagg School of Pharmacy and Pharmaceutical Sciences. Dr. Watanabe argued that Medicare is unable to negotiate for lower prices like the U.S. Department of Veterans Affairs.

Dr. Watanabe's interview with NBC7 can be viewed here.

You can read my piece here.

Communicating data effectively with data visualizations - Part 7 (Using Small Multiples or Panel Charts in Excel)

BACKGROUND

It can be challenging when you’re trying to visualize many different groups using the same metric repeatedly. Initially, you may want to do this with a single figure, but this is too crowded and prevents you from seeing the differences across the groups. Alternatively, you can separate and visualize the groups individually without compromising the space or size of the figure. In this article, we will discuss the use of small multiples or panel charts in Excel. This will make it easier for the eyes to see the differences while presenting a large number of data.

MOTIVATING EXAMPLE

I have created a data set that contains the average temperature (degrees F) across four quarters for eight states in the United States. These temperatures were generated using a random number generator.

The data has the following structure:

Using this data, we can generate a single plot that contains all the states and their average temperature for each quarter.

There are several issues with this plot. First, there is so much clutter, it is difficult to discern which states are increasing or decreasing over time. Second, the colors, despite being different, seem to mix in too much like spaghetti. In fact, this is commonly called a “spaghetti” plot.[1]

To avoid this cluster of tangled lines, it is best to view these lines separately in small multiples. We can apply the principle of small multiples into an 8 by 1 matrix (8 rows and 1 column of data). 

By separating each state into its own separate line, we can identify which states had temperatures that increased across time. From this figure, we can see that Alabama, Alaska, Arizona, and Kansas have temperatures that increased from Q1 to Q4. However, the magnitude in the change for Kansas looks similar to Alaska (absolute difference of 37 degrees F and 76 degrees F, respectively). Despite using the same Y-axis, the compressed scale gives the illusion that all the changes were similar in magnitude, which they were not.

We can improve upon this figure by furthering the use of small multiples. Tufte argues that small multiples can present a large amount of comparisons through repeated panels.[2] With this in mind, we can take the above figure and separate each state into a 2 by 4 matrix.

This is vastly improved. We can see trajectory for each state across the quarters. For example, we can clearly see that Alabama, Alaska, Arizona, and Kansas have temperatures that were increasing steadily across time. However, large fluctuations in temperatures were observed for New Jersey, New York, and Oklahoma. Only California appears to have a steady trend in the temperature across time.

The panel chart has equal sized boxes with temperature scales that are identical. This allowed our eyes to make quick comparisons between the states. Moreover, we can also identify the trends much more easily that in the “spaghetti” plot.

TUTORIAL: PANEL CHARTS (SMALL MULTIPLES)

To generate the above panel chart, we will use the randomly generate temperature dataset, which can be downloaded from here.

An important element of the dataset is the column called “strata.” This column will allow us to generate a staggered line plot separated by the strata.

The following figure illustrates the different variable names including the strata column.

Notice how the strata column alternates between 1 and 2? This will be used to separate the temperatures of each state into clusters. In other words, we will cluster the temperature from Q1, Q2, Q3, and Q4 for each state.

Once you’ve reviewed the data, select all the data and then use the pivot table feature to insert the new table onto a different worksheet.

Excel will automatically create a new worksheet with a blank pivot table work space. You can use this work space to generate different tables using the powerful pivot table features.

We will use the pivot table builder to generate the table we need for the panel chart. After you insert the pivot table into a new worksheet, move the State variable into the Row box followed by the Quarter variable. (This is denoted by A.) Move the Temperature variable into the Values box. (This is denoted by B.) Then move the Strata variable into the Columns box. (This is denoted by C.) Review your work with the following figure below.

Once you set up you pivot table, you should notice that the temperature values are staggered between the states. This is important for when you construct the line graphs for the panel charts.

Next, we will remove the Grand Total column. This isn’t important for us, so let’s right click the cell that contains the column header Grand Total and select Hide.

Then click on the Design tab on the ribbon and select Report Layout > Show in Tabular Form. This will change the design of the default pivot table.

Next, we are going to remove the total rows for each state. Right click on the first state (Alabama) and select Hide. You should notice that the total row for each state is now hidden. This updated pivot table design will make it easier to create panel charts.

You pivot table should look like the following:

Copy and paste this table and its values onto a blank section of the worksheet. Then highlight the data for the first four states and insert a line chart.

You will see the trend lines for the four states, which will be separated by the different time periods.

There are two colors for the alternating states. Change this to a single color (e.g. Blue). Then remove the gridlines, chart title, and the legend. The chart should look like the following:

The next part will be to include line partitions between each state, which will allow the eye to distinguish each line as separate trends for the states.

We will need to create a new dataset for the line partitions. To do that, count the number of time periods for one of the states (the time periods should be equivalent for all the states. In our case, there are four quarters for each state). In between Q4 and Q1, there is a gap. If you take all the quarters from Q1 and Q4 for Alabama to California, there are a total of 16 intervals. In between interval 4 and 5 is where we want to put first line partition. Interval 8 to 9 is where we want to put the second line partition, etc. For this example, the dataset should look like the following:

Select the chart and click on the Chart Design tab and click on Select Data.

The Select Data Source window will appear and list the previous data already used to generate the trend lines for each state. We will add a new dataset (A) and select the Y values from the dataset that was generated for the partitions (B). 

This will create a line at the bottom of the chart area.

Right click on the line (A) and select Change Chart Type > X Y (Scatter) > Scatter (B).

Right click on the scatter and go to Format Data Series > Series Options > Plot Series On > Secondary Axis.

Select the Y-axis on the right side of the chart (A).

Then go to Format Axis > Axis Options and set the Maximum to 1.0.

Next, we will align the scatter points into the correct partition. Right click on the chart area and click on Select Data. Select Series 3 and go to the X values box. In the X values box, select the data in the Partition column.

The scatter points appear to be in the correct location. The next steps will involve including error bars for the partition lines and formatting.

Click on scatter points and select Chart Design in the Ribbon. Click on the Add Chart Element and select Error Bars > More Error Bars Options….

Format the error bars and remove the cap. Depending on where the scatter points are, you want to choose error bars that will cover the empty region. In our example, the scatter points are at the top, so having the “Minus” or “Both” direction options will work for us. We will leave it at “Both” for this example.

Click on the horizontal error bars and delete them.

Click on the scatter point and go to the Format Data Series. Go to the Fill & Line > Marker Options > None.

The chart should look like the following:

The remainder of this tutorial will be to make this aesthetically appealing.

We want to hide the secondary Y-axis, which can be done by hiding the line and change the font color to match the background. Then we want to change the size of the chart using the Chart Options.

We also changed the font to Helvetica (native to Apple products), resized the chart boxes, included a Vertical Y-title bar for the temperature axis, added a mean Temperature band using 60% transparency, change the color of the vertical error bars to a lighter gray, changed font size on the Y-axis, and moved the X-axis labels to the top. We repeated these steps for the final four states and carefully placed it below the first four states, using the grid to assist with alignment.

The final panel chart:

CONCLUSIONS

When you encounter a data set that can be separated into smaller graphics, consider using the small multiple principle or panel charts approach. It requires a little more work, but the results can provide a narrative that is easy to visualize and interpret. In our example, we start to notice different trends using different approaches to the small multiple principle. It’s best to experiment which ones work best for your needs. Here are some examples of small multiples that may inspire you: link1 and link2.

REFERENCES

1. Knaflic CN. Strategies for avoiding the spaghetti graph. Storytelling with data. http://www.storytellingwithdata.com/blog/2013/03/avoiding-spaghetti-graph. Published March 14, 2013. Accessed May 16, 2018.

2. Tufte ER. The Visual Display of Quantitative Information. Second. Cheshire, CT: Graphics Press, LLC.; 2001.

Communicating data effectively with data visualizations - Part 6 (Tornado diagram)

BACKGROUND

Suppose you had some results and you were interested in whether or not these findings were sensitive to change. You can illustrate these effects using a tornado diagram, which uses bar charts to compare the change from the original findings. In other words, tornado diagrams are useful to illustrate a sensitivity analysis.

In this tutorial, we will provide you with a step-by-step guide on how to graph a tornado diagram from a sensitivity analysis.

MOTIVATING EXAMPLE

Imagine that you are planning a vacation, and you allocated $6,000 for the trip. You perform some cost estimates and find a vacation package that costs $5,050, which is within your budget. But then you see some deals and some extra luxuries that you want to add to your current vacation package. Some of these will change the cost of your original cost estimates. In order to see which of these additional deals or luxuries would impact your cost estimates, you decide to perform a one-way sensitivity analysis. That is, you change the cost of one variable at a time to see how it effects your original cost estimates (e.g., base-case).

Table 1 summarizes your base-case vacation costs and the possible changes due to the additions of deals and luxuries.

The “Low input” or “deals” reduce the total cost of your vacation. The “High input” or luxuries increase the cost of your vacation.

You want to visualize if any of these adjustments will change your original cost estimates (e.g., $5,050).

BUILDING A TORNADO DIAGRAM

A tornado diagram can be used to visualize these additional changes to the variables.

Step 1: Open Excel and insert a clustered bar chart

Step 2: Enter data for the “Low input”

Right-click on the empty chart area and select “Name” and enter “Low input.” Then in the “Y values:” box, select all the values in the “Low result” column of your table. In the Horizontal (Category) axis labels:” highlight the variable names under the “Base-case results” column. The figure below illustrates the correct selections for each input box.

Step 3: Enter data for the “High input”

Repeat same steps for the “High input” data range.

Step 4: Center the axis at the estimated cost

Right-click on the X-axis and go to the Format Axis > Vertical Axis Crosses > Axis Value and enter “5050.” This will center the axis at the estimated cost of $5,050.

Step 5: Move the variable names to the left side of the plot

After centering the axis on the estimate cost of $5,050, you can start to see the beginnings of a tornado diagram. However, the variable names are in the way. To relocate these, Right-click on the Y-axis and select the Axis Options > Interval Between Labels and select “Low.” This will move the variable names to the left side so that it doesn’t interfere with the bars in the middle of the chart.

Step 6: Align the bars so that they are next to each other

The bars are not aligned with each other. You can align them using the series overlap option. Right-click on one of the bars and go to Series Options > Plot Series On and enter 100 on the “Series Overlap” widget. After you press Enter, the bars should be aligned with each other.

Step 7: Sort and change fonts

To complete the tornado diagram, you can sort the bars so that the largest change is at the top and the smallest change is at the bottom (looks like a tornado). Right-click on the Y-axis and got to Format Axis > Axis Options > Axis Position and check the box “Categories in reverse order.” This will order your diagram to look more like a tornado.

Step 8: Final changes and edits

The last steps improve the aesthetics. Changing the fonts and colors can improve the tornado diagram.

CONCLUSIONS

The tornado diagram tells us that paying for an additional “luxury” for the cost of the flight will exceed our budget of $6,000 (indicated by dotted red line). As a result, we will not spend extra capital to upgrade our seats! However, we can splurge a little when it comes to other elements of our trip (e.g., expensive meals, luxury vehicle rental, or additional excursions).

REFERENCES

I used the following guide developed by Excel Champs to develop this this blog.

 Note: Updated on 11 July 2022